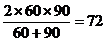In this article, we will discuss the concepts, formulas and some questions based on speed, time and distance. As Time, Speed and Distance forms an integral part of every competitive exam, you cannot afford to skip this topic.
Speed
Speed basically tells us how fast or slow an object moves.
It is described as the distance travelled by an object divided with the time taken to cover that distance.
Speed = Distance/Time
This shows that Speed is directly proportional to distance but inversely proportional to time.
Distance = Speed * Time and,
Time = Distance/Speed
Example: What is the distance covered by a car travelling at a speed of 40 kmph in 15 minutes?
Solution:
Distance= speed* time= 40*15/60=10 km.
The important point to note is that time given was in minutes, whereas the speed was in kmph.
Therefore, either speed has to be converted to km/min or time has to be expressed in hours.
We have converted time in hours.
15 min=15/60 hours.
Average Speed
Case 1: When Time is Constant
The average speed of travelling at two different speeds for the same time span is just the simple average of two speeds.
Let Speed 1 be x km/hr
Let Speed 2 be y km/hr
Therefore,
Average Speed when time is same = (x+y)/2
Example: A car is travelling at an average speed of 45kmph for the 1st hour and at 65 kmph for the next 1 hour. Calculate his average speed.
Solution:
As the time is same, i.e. 1 hour,
Average speed= (45+65)/2= 55 kmph.
Must Read Time, Speed and Distance Articles
Case 2: Average Speed When Distance is Constant
Average Speed = 2ab/(a+b) (where a and b are two speeds)
Let us understand how this came.
Let the two speeds be a km/hr and b km/hr.
Let the distance travelled in each of the speeds be x km.
As we know that, Time = Distance/Speed
Hence, time taken to cover x km at a km/hr will be x/a hrs
And, time taken to cover x km at b km/hr will be x/b hrs
Total time taken = x/a+x/b =(bx+ax)/ab = x(b+a)/ab
And the total distance covered = 2x
Therefore,
Average Speed =

Example: On his way to office, Big Bull was travelling at 30 kmph and on the return journey, he was travelling at 45kmph. What is Big Bull's average speed?
Solution:
37.5 kmph is incorrect as the time travelled is different in both the cases and only the distances are same.
Let distance = x km
Therefore, Time taken on Big Bull's onward journey =x/30 hours and
Time taken on his return journey=x/45 hours
Therefore, total time = (x/30)+ (x/45) hours.
Total distance = 2x km
Average speed=
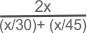
kmph = 36kmph
Important Time and Distance Conversions
1 km = 1000 meters
1 meter = 100 cm
1 hour = 60 minutes
1 min = 60 seconds
1 hours = 3600 seconds
1 km/hr =

m/sec
Hence, 1 m/sec =

km/hr
1 mile = 1760 yards
1 yard = 3 feet
1 mile = 5280 feet
1 mph =

yards/sec
1 mph =

ft/sec
Now, let us try doing some questions.
Solved Questions
Question 1: What is the distance covered by a car travelling at a speed of 40 kmph in 15 minutes?
Solution:
We know that 1 hour = 60 minutes
Therefore, 15 minutes = 1/4 hours (because 15/60 = 1/4)
Distance = Speed * Time
Distance = 40 * (1/4) = 10 kms
Question 2: A car is travelling at a speed of 50 kmph. How long will it take to travel 60 kms?
Solution: Distance = Speed * Time
60 = 50 * T
T = 1.2 hrs or 1 hr and 12 minutes
Question 3: Walking at 5/6th of his usual seed, Raman reached his destination 10 minutes late. Find his usual time and he times taken on this occasion.
Solution:
Let his usual speed be x km/hr and his usual time be t hours
His time on this occasion is
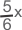
The time taken is

hrs
Since the distance travelled on both occasions is the same,
xt =
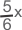
*

( because, Distance = Speed * Time)
Solving for t, we get t = 5/6hrs
= 50 minutes and the time taken on this occasion = 50 + 10 = 60 minutes
Question 4: While going to office, Rajat travels at a speed of 60 kmph and on his way back, he travels at a speed of 90 kmph. What is his average speed of the whole journey?
Solution: When distance travelled is same, then average speed = 2ab/(a+b)(where a and b are two different speeds)
Therefore Average Speed =
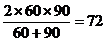
Average Speed = 72 kmph
Question 5: A CTU bus and an ordinary bus leave Chandigarh for Ambala- a distance of 32 km simultaneously. The ratio between the average speed of the CTU bus and that of the ordinary bus is 3:2. The CTU bus reaches Ambala and immediately leaves back for Chandigarh and meets the ordinary Bus at Lalru. What is the distance between Ambala and Lalru?
Solution: Speed of CTU bus : Speed of ordinary bus :: 3:2
As Distance ∞ Speed
Distance travelled by CTU bus : Distance travelled by ordinary bus :: 3:2
Let the distance travelled between Ambala and Lalru be x km
Then the distance travelled by CTU bus = 32 + x
While the distance travelled by ordinary bus = 32 – x
Therefore, 32 + x : 32 – x :: 3:2
Solving for x, we get x = 6.4 km (i.e. the distance between Ambala and Lalru)
Question 6: Travelling at 6 kmph, Niharika reaches her office 20 minutes late. Travelling at 8 kmph, she reaches her office 30 minutes early. What is her usual speed and time taken to reach her office?
Solution: Let her usual speed be S kmph and her usual time be t hours
Therefore,

Solving for t, we get t = 3 hrs
Since the usual time taken = 3 hrs, usual distance travelled = 3S kms
Equating distance travelled usually, with distance travelled at any of the other two speeds, we get 6 * (3+20/60) = 3S
Therefore, S = 6

kmph
Question 7: How much time will a 360 meters long train running at 108 kmph will take to cross a standing electricity pole?
Solution: We know that, 1 km/hr = 5/18 m/sec
Hence, 108 kmph = 108 *

m/sec = 30 m/sec
Distance = Speed * Time
360 = 30 * Time
Time = 12 secs

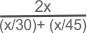 kmph = 36kmph
kmph = 36kmph m/sec
m/sec km/hr
km/hr yards/sec
yards/sec ft/sec
ft/sec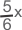
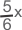 *
*