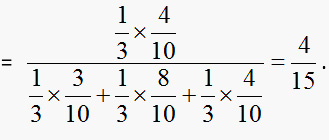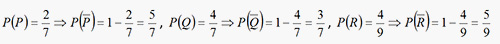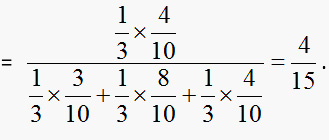Probability: Solved Examples

Example 2: Find the probability of getting a numbered card when a card is drawn from the pack of 52 cards.
Sol: Total Cards = 52. Numbered Cards = (2, 3, 4, 5, 6, 7, 8, 9, 10) 9 from each suit 4 × 9 = 36
P (E) = 36/52 = 9/13

Example 3: There are 5 green 7 red balls. Two balls are selected one by one without replacement. Find the probability that first is green and second is red.
Sol: P (G) × P (R) = (5/12) x (7/11) = 35/132

Example 4: What is the probability of getting a sum of 7 when two dice are thrown?
Sol:  Probability math - Total number of ways = 6 × 6 = 36 ways. Favorable cases = (1, 6) (6, 1) (2, 5) (5, 2) (3, 4) (4, 3) --- 6 ways. P (A) = 6/36 = 1/6

Example 5: 1 card is drawn at random from the pack of 52 cards.
(i) Find the Probability that it is an honor card.
(ii) It is a face card.
Sol: (i) honor cards = (A, J, Q, K) 4 cards from each suits = 4 × 4 = 16
P (honor card) = 16/52 = 4/13
(ii) face cards = (J,Q,K) 3 cards from each suit = 3 × 4 = 12 Cards.
P (face Card) = 12/52 = 3/13

Example 6: Two cards are drawn from the pack of 52 cards. Find the probability that both are diamonds or both are kings.
Sol: Total no. of ways = ⁵²C₂
Case I: Both are diamonds = ¹³C₂
Case II: Both are kings = ⁴C₂ 
P (both are diamonds or both are kings) = (¹³C₂ + ⁴C₂ ) / ⁵²C₂

Example 7: Three dice are rolled together. What is the probability as getting at least one '4'?
Sol: Total number of ways = 6 × 6 × 6 = 216. Probability of getting number ‘4’ at least one time
= 1 – (Probability of getting no number 4) = 1 – (5/6) x (5/6) x (5/6) = 91/216

Example 8: A problem is given to three persons P, Q, R whose respective chances of solving it are 2/7, 4/7, 4/9 respectively. What is the probability that the problem is solved?
Sol: Probability of the problem getting solved = 1 – (Probability of none of them solving the problem)

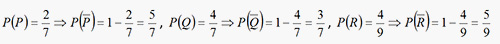
Probability of problem getting solved = 1 – (5/7) x (3/7) x (5/9) = (122/147)

Example 9: Find the probability of getting two heads when five coins are tossed.
Sol: Number of ways of getting two heads = ⁵C₂ = 10. Total Number of ways = 2⁵ = 32
P (two heads) = 10/32 = 5/16

Example 10: What is the probability of getting a sum of 22 or more when four dice are thrown?
Sol: Total number of ways = 6⁴ = 1296. Number of ways of getting a sum 22 are 6,6,6,4 = 4! / 3! = 4
6,6,5,5 = 4! / 2!2! = 6. Number of ways of getting a sum 23 is 6,6,6,5 = 4! / 3! = 4.
Number of ways of getting a sum 24 is 6,6,6,6 = 1.
Fav. Number of cases = 4 + 6 + 4 + 1 = 15 ways. P (getting a sum of 22 or more) = 15/1296 = 5/432

Example 11: Two dice are thrown together. What is the probability that the number obtained on one of the dice is multiple of number obtained on the other dice?
Sol:Total number of cases = 6² = 36
Since the number on a die should be multiple of the other, the possibilities are
(1, 1) (2, 2) (3, 3) ------ (6, 6) --- 6 ways
(2, 1) (1, 2) (1, 4) (4, 1) (1, 3) (3, 1) (1, 5) (5, 1) (6, 1) (1, 6) --- 10 ways
(2, 4) (4, 2) (2, 6) (6, 2) (3, 6) (6, 3) -- 6 ways
Favorable cases are = 6 + 10 + 6 = 22. So, P (A) = 22/36 = 11/18

Example 12: From a pack of cards, three cards are drawn at random. Find the probability that each card is from different suit.
Sol: Total number of cases = ⁵²C₃
One card each should be selected from a different suit. The three suits can be chosen in ⁴C₃ was
The cards can be selected in a total of (⁴C₃) x (¹³C₁) x (¹³C₁) x (¹³C₁)
Probability = ⁴C₃ x (¹³C₁)³ / ⁵²C₃
= 4 x (13)³ / ⁵²C₃

Example 13: Find the probability that a leap year has 52 Sundays.
Sol: A leap year can have 52 Sundays or 53 Sundays. In a leap year, there are 366 days out of which there are 52 complete weeks & remaining 2 days. Now, these two days can be (Sat, Sun) (Sun, Mon) (Mon, Tue) (Tue, Wed) (Wed, Thur) (Thur, Friday) (Friday, Sat).
So there are total 7 cases out of which (Sat, Sun) (Sun, Mon) are two favorable cases. So,  P (53 Sundays) = 2 / 7
Now, P(52 Sundays) + P(53 Sundays) = 1
So, P (52 Sundays) = 1 - P(53 Sundays) = 1 – (2/7) = (5/7)

Example 14: Fifteen people sit around a circular table. What are odds against two particular people sitting together?
Sol: 15 persons can be seated in 14! Ways. No. of ways in which two particular people sit together is 13! × 2!
The probability of two particular persons sitting together 13!2! / 14! = 1/7
Odds against the event = 6 : 1

Example 15: Three bags contain 3 red, 7 black; 8 red, 2 black, and 4 red & 6 black balls respectively. 1 of the bags is selected at random and a ball is drawn from it. If the ball drawn is red, find the probability that it is drawn from the third bag.
Sol: Let E1, E2, E3 and A are the events defined as follows.
E1 = First bag is chosen
E2 = Second bag is chosen
E3 = Third bag is chosen
A = Ball drawn is red
Since there are three bags and one of the bags is chosen at random, so P (E1) = P(E2) = P(E3) = 1 / 3
If E1 has already occurred, then first bag has been chosen which contains 3 red and 7 black balls. The probability of drawing 1 red ball from it is 3/10. So, P (A/E₁) = 3/10, similarly P(A/E₂) = 8/10, and P(A/E₃) = 4/10. We are required to find P(E₃/A) i.e. given that the ball drawn is red, what is the probability that the ball is drawn from the third bag by Baye’s rule