Percentages: Concepts & Tricks
A decimal fraction is one in which the denominator of the fraction is a power of 10 i.e. 10, 100, 1000 etc. That decimal fraction which has 100 as its denominator is known as Percentage. The numerator of such a fraction is known as Rate Per Cent.
15 % and 15/100 mean one and the same quantity.
Any number written in the form of a fraction with 100 as the denominator is a percentage.
For example: 13 = 1300/100 = 1300%
3/5 = 60/100 = 60%
62.5/100 = 62.5%
Alternatively, X% of a number Y = (X × Y)/100
For example: 16(2/3) % of 300 = (50/3) × (300/100) = 50
A. Conversion from a Fraction to Percent and vice versa
1. Fraction to Percent: Multiply the fraction by 100 to convert it into a percent.
E.g.: 0.5 = 0.5 x 100 = 50 %
5/8 = 5/8 × 100 = 62.5 %
2. Percent to Fraction: Reversing the earlier operation converts a percent to a fraction - i.e. divide the percent by 100.
e.g. 60 % = 40/100 = 0.6
65 % = 65/100 = 0.65
B. Percentage Increase or Decrease of a Quantity:
Here, one point is to be noted, that the increase or the decrease is always on the original quantity. If the increase or decrease is given in absolute and the percentage increase or decrease is to be calculated, then the following formula is applied to do so.
% increase /decrease = 100 × Quantity increase or decrease / original quantity
The point worth remembering is that the denominator is the ORIGINAL QUANTITY.
e.g. The salary of a Rakesh goes up from Rs 100 to Rs 135. What is the percentage increase in his salary?
Increase = 135 – 100 = Rs. 35.
∴ % increase =35/100 × 100% = 35 %
Alternatively, if the salary of the man had been reduced from Rs. 145 to Rs 100, what is the percentage decrease in his salary?
Decrease = 145– 100 = Rs. 45
∴ % decrease = 45/145 × 100% = 31.03 %.
Note that for the same quantity of increase or decrease the % increase and % decrease have two different answers. The change in the denominator i.e. the original value changes in the above two situations and hence the difference.
Must Read Percentages Articles
C. To Increase a Number by y %:
If a number is increased by 10 %, then it becomes 1.1 times of itself.
If a number is increased by 30 %, then it becomes 1.3 times of itself.
D. To Decrease a Number by y %:
If a number is decreased by 10 %, then it becomes 0.90 times of itself.
If a number is decreased by 30 %, then it becomes 0.70 times of itself.
E. Equivalent Percentages using Fractions:
| 1/2 |
50% |
3/4 |
75% |
2/9 |
22(2/9)% |
| 1/3 |
33(1/3)% |
4/5 |
80% |
1/15 |
6(1/3)% |
| 1/4 |
25% |
1/8 |
12(1/2)% |
1/20 |
5% |
| 1/5 |
20% |
1/12 |
8(1/3)% |
1/25 |
4% |
| 1/6 |
16(2/3)% |
3/8 |
37(1/2)% |
1/50 |
2% |
| 2/5 |
40% |
5/8 |
62(1/2)% |
4/3 |
133(1/3)% |
| 3/5 |
60% |
7/8 |
87(1/2)% |
5/4 |
125% |
| 2/3 |
66(2/3)% |
1/9 |
11.11% |
6/5 |
120% |
F. Income/Weight/Salary More
If Pankaj’s salary is R % more than Rohan, then Rohan’s salary is less than that of Pankaj by 100 × R/ (100 + R) %.
G. Income/Weight/Salary Less
If P’s income is R% less than Q, then Q’s income is more than that of P by 100 × R/(100 – R) %
Given below are some important results in that context:
- If A is 16(2/3) % less than B, then B is 20 % more than A.
- If A is 20% less than B, then B is 25 % more than A.
- If A is 25 % less than B, then B is 33(1/3) % more than A.
Note: If the question is - the price of a commodity is increased by R %, by what percent should its consumption be decreased, so that the total expenditure remains the same. Then the way to solve such question is the same. I.e., if the price is increased then consumption should be decreased by 100 X R/(100 + R). If the price is decreased, then consumption should be increased by 100 X R/(100 + R)
H. Increase and Decrease by the same % age.
If a number is increased by R %, and then it is decreased by R %, then in total there would be a decrease of R2/100 %.
I. Increase and Decrease by different% age.
If there is X percent increase and then Y percent decrease in a value, then net percentage change =
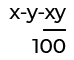
The above-mentioned formula is very important. It has its application in so many other questions. In case instead of increase, there is a decrease, simply put a negative value in its place. You will get the right answer, even when both the decreases are given. What you will get after solving the formula, if it is positive, there is an increase, and if it is negative, there is a decrease.
J. Compound Growths.
Typically compound growths are used in investment growth analysis (compound interest) or in population growth (things like cattle population, steel production output growth). In this section, we will be primarily concerned with compound growth related to population.
If P is the population of a country and it grows at r % per annum, then the population after n years will be:
A = P [(100+r) / 100]n