Q.1. Two circles with same centre P have radii 6.5 cm and 3.3 cm. Through a point A of the larger circle, a tangent is drawn to the smaller circle touching it at B. Find AC.
A. 8.3 cm
B. 11.2 cm
C. 5.5 cm
D. 16.7 cm
Answer: Option B
Sol :
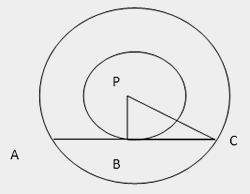
∠PBC = 90° (A tangent is perpendicular to the radius at the point of contact)
So (6.5)
2 = (3.3)
2 + (BC)
2.
So BC = 5.6. Hence AC = 2 × 5.6 = 11.2 cm.
Q.2. Find the area of the circle having center at (5, 7) and passing through (2, 3).
A. 16π
B. 20π
C. 21π
D. 25π
Answer: Option D
Sol :
Centre at (5, 7) and passing through (2, 3). So, radius of circle is r =√(2-5)2 + (3-7)2 = 5. So, the area of circle = 25π.
Q.3. In a circle of radius 10, A & B are two points on the circumference. If arc AB is 120°, what is the length of line segment AB?
A. 10√3;
B. 10
C. 5√3;
D. None of these
Answer: Option C
Sol :
Half of the triangle formed between A, B and the centre of the circle will be a 30 – 60 – 90 triangles. Since 10 (the radius) is the hypotenuse of this triangle, half of AB will be 10 × √3 / 2 = 5√3.
Q.4. AB is a chord of the circle with centre O such that the length of the minor arc AB is 2π metres. If ∠AOB = 90°, what is the area of the minor sector AOB?
A. 24πm2
B. 4πm2
C. 16πm2
D. 6πm2
Answer: Option B
Sol :
Since the central angle is 90° and the length of the corresponding arc is 2π, the circumference of the circle is 8π. So the radius of the circle is 4 m. The area of the sector is therefore ¼ × π × 42 = 4π m2.
Q.5. AP is tangent at point P to the circle with centre O and diameter BC. If AP = 20 and AB = 10, what is the length of AO?
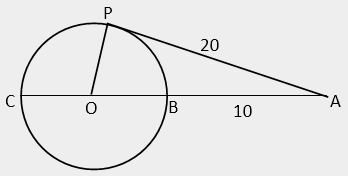
Answer: Option A
Sol :
Suppose OP = r. Then, OA = 10 + r.
In ΔAPO, (10 + r)2 = 400 + r2.
Solving this equation gives r = 15. So, AO = 10 + 15 = 25.
Must Read Circle Articles
Q.6. In the figure, P, Q and R are the centres of 3 circles such that P, Q and R are collinear. What is the ratio of the area of the entire shaded region to the area of the unshaded region?
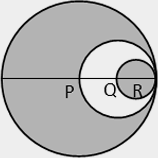
A. 5:2
B. 17:4
C. 13:3
D. 17:3
Answer: Option C
Sol :
If the radius of circle R is r, then the radii of circles P and Q are 4r and 2r respectively. The unshaded region is 4πr2 – πr2 = 3πr2. The entire shaded region is 16πr2 – 3πr2 = 13πr2. The ratio is 13: 3.
Q.7. A chord AB of a circle of radius 10.5 cm makes an angle of 120° at the centre of the circle. Find the area of the minor segment approximately.
A. 62.5 cm2
B. 60.25 cm2
C. 67.7 cm2
D. 61.5 cm2
Answer: Option C
Sol :
As the central angle is given to be 120°, you must quickly realize that it will result into an equilateral triangle.
Now area of the minor sector: π × (10.5)2 &time' 120 / 360 = 115.4
Area of equilateral triangle = (10.5)2 × √3/4 = 47.7
The difference of the two represents the area of the minor segment (Note: it is not a sector)
i.e. 115.4 – 47.7 = 67.7 cm2
Q.8. Find the approximate area of the major segment as per the information given in the above question?
A. 278.5 cm2
B. 242.25 cm2
C. 262 cm2
D. 247 cm2
Answer: Option A
Sol :
The area of the major segment
= Area of the circle – area of the minor segment → × × (10.5)2 = 346.2.
Area of major segment = 346.2 – 67.7 = 278.5 cm2.
Q.9. It is not possible to draw a circle having its centre on a fixed straight line M and passing through two fixed points P and Q not on M if
A. M is parallel to PQ
B. M is the perpendicular bisector of PQ
C. M is perpendicular to PQ but does not bisect it
D. M is not perpendicular to PQ but bisects it
Answer: Option C
Sol :
In all the remaining cases, except (C), we can draw at least one circle that is on M and passes through P and Q. In case M is perpendicular to PQ, but does not bisect it, then we will have no point on M that is equidistant from both P and Q.
Q.10. Two small circular parks of diameters 32 m and 24 m are to be replaced by a bigger circular park. What would be the radius of this new park, if the new park has the same area as the two small parks?
Answer: Option D
Sol :
Area of the new circular park = Sum of the areas of the 2 smaller parks ⇒ π (32/2)2 + π (24/2)2 = π(256 + 144) = 400 π ⇒ 400 π = πR2. ∴ R2 = 400 ⇒ R = 20m.


