A circle is a set of points in a plane that are located at a same distance from the fixed point (the center of the circle).
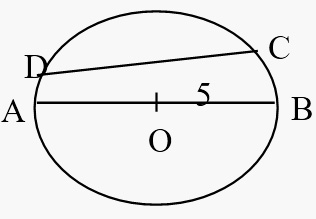
In the above circle, O is the center of the circle and AB and CD are chords. AB is the diameter and OB is the radius. If OB = 5, then the perimeter of circle or circumference of circle is 2π(5) = 10π, and area of circle is π(5)2 = 100π.
Arc: It is a part of circle. A major arc is an arc greater than the semicircle and a minor arc is an arc less than the semicircle.
Congruent Circles : Circles with equal radii are called congruent circles.
Concentric Circles : Circles having a same centre are called concentric circles.
Tangent Circles : The circles lying in same plane and touching externally at one point are called tangent circles.
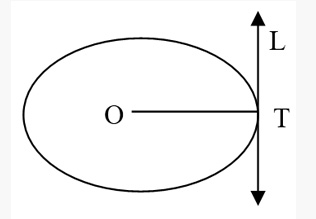
A line that is perpendicular to the diameter or radius of circle at a point of contact on circle is called tangent. The line L is tangent to circle and radius OT is perpendicular to line L.
If every vertex of a polygon lies on the circle, then the polygon is inscribed in the circle and the circle is called circumscribed. If every side of the polygon is tangent to the circle, then the polygon is circumscribed about a circle and the circle is inscribed in the polygon.
In the figure above, quadrilateral PQRS is inscribed in the circle and hexagon ABCDEF is circumscribed about the circle.
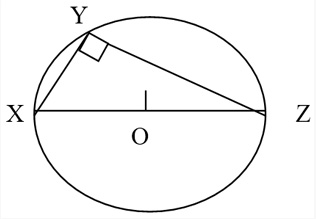
If a triangle is inscribed in the circle so that one of its sides is the diameter of circle, then the triangle is a right triangle. In the above circle, XZ is diameter and the measure of angle XYZ is 90°.
Must Read Circle Articles
Some Important Properties of Circles:
- The perpendicular from the centre of a circle to the chord of circle bisects the chord.
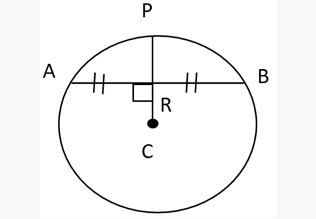
Conversely, the line joining the centre of a circle and the midpoint of a chord is perpendicular to the chord.
- Congruent circles or equal chords are equidistant from the centre.
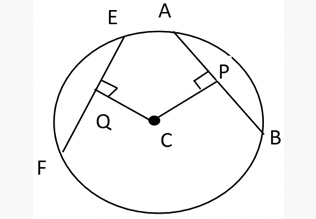
Conversely, two chords of a circle or congruent circles that are equidistant from the centre are equal. Two chords PQ, RS intersect at a point then CP × CQ = CR × CS
- In a circle or congruent circles, equal chords subtend equal angles at centre.
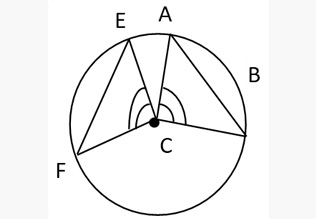
Conversely, chords, which subtend equal angles at the centre of the congruent or same circles, are equal.
- If two circles touch each other externally, distance between their centres = sum of their radii.
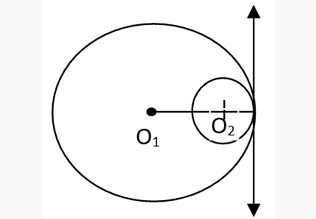
If two circles touch each other internally, the distance between their centers = difference of their radii.
- The measure of an inscribed angle is half of the measure of its intercepted arc. ( Inscribed angle theorem). ∠ACB = ½ arc (ADB) = ½ ∠AOB.
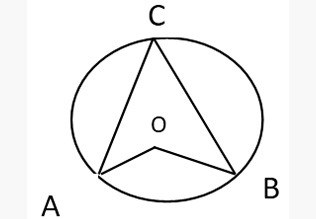
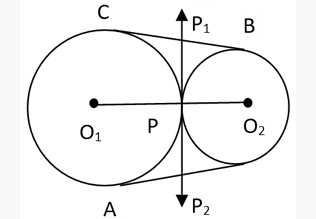
Angles subtended are the same segments are equal:
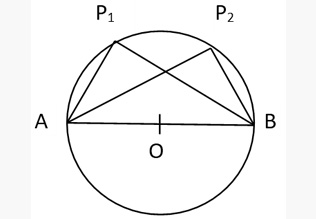
∠AP1B = ∠AP2B. Angle subtended in a semicircle is 90°
i.e ∠AP1B = 90° = ∠AP2B
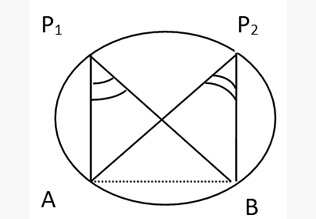
Angle subtended in a minor segment is obtuse and that in a major segment is acute.
 ∠AP1B > 90° & ∠AP2B < 90°
∠AP1B > 90° & ∠AP2B < 90°
- For two circles with centres A and B, RS and PQ are the direct common tangents, and EF and CD are the transverse common tangents.
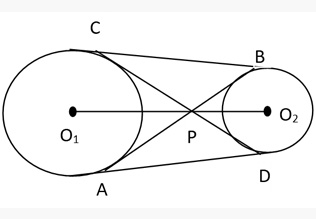
(Only two of both transverse common tangents and direct common tangents are possible.)
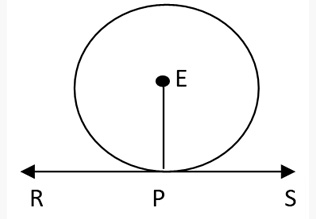
Tangent is always perpendicular to the line joining the centre and the point of tangency.
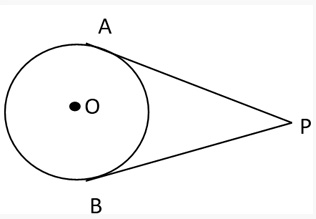
Two tangents from the same external point are equal in length. PA = PB
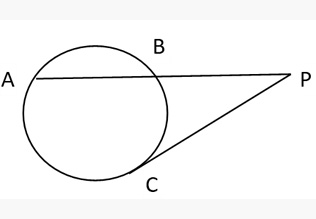
If AB is a chord of a circle and PC is the tangent (both for a external point P) than PA × PB = PC2
- Length of direct common tangent = √(distance between centers)2 - (r1 - r2)2
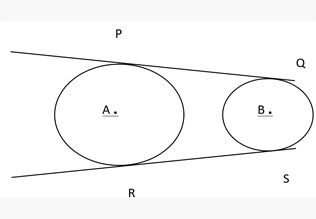
- Length of transverse common tangent = √(distance between centers)2 - (r1 + r2)2
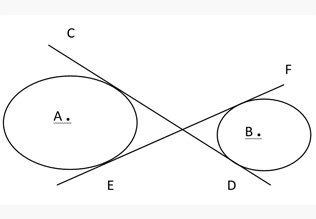
- Alternate Segment Theorem:
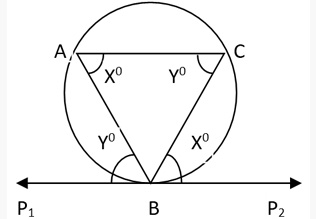
Angle between any chord (at the point of tangency) and the tangent is equal to the angle subtended by the chord at any point on the other side of the segment (alternate segment).
In the fig ∠CBP2 = ∠CAB = X° & ∠P1BA = ∠ACB = Y°
Cyclic Quadrilaterals:
A quadrilateral is said to be cyclic if opposite angles of the quadrilateral are supplementary and all of its vertices are on the circle. The points lying on a circle are called co cyclic.
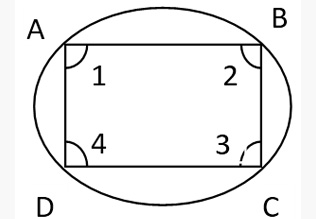
The opposite angles of a cyclic quadrilateral are supplementary. Conversely, if the opposite angles of a quadrilateral are supplementary, then it is a cyclic quadrilateral.
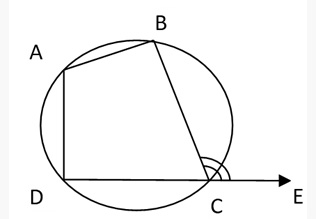
An exterior angle of a cyclic quadrilateral is equal to the angle opposite to its adjacent interior angle. ∠BCE = ∠DAC.
For any cyclic quadrilateral, sum of product of two pairs of opposite sides equals the product of diagonals.
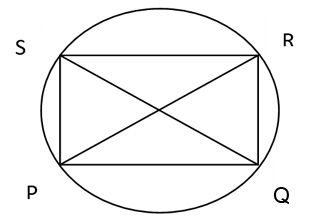
PQ × RS + QR × SP = PR × SQ.
The area of a cyclic quadrilateral = √(s-a)(s-b)(s-c)(s-d) where s is the semi perimeter and a, b, c and d are sides of the quadrilateral.
Area of a cyclic quadrilateral in which a circle can be inscribed =√a×b×c×d , where a, b, c and d are the sides of the quadrilateral.
Sectors of a Circle:
The number of degrees of arc in a circle (or the number of degrees in a complete revolution) is 360.
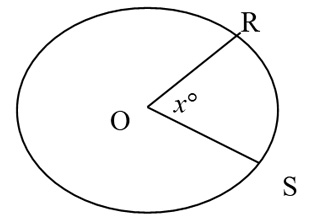
In the above circle with center O, the length of arc RS is x/360 of the circumference of the circle; for example, if x = 60°, then arc RS has length 1/6 of the circumference of the circle. We can remember the following formulas:
- Length of arc RS = 2πr × x/360. ∵ The complete circle is having 360 degrees & any part of it shall be equal to x/360.
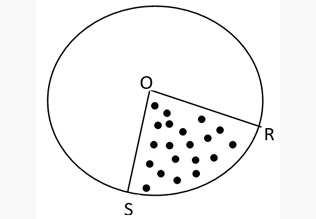
- Area of Sector ORS = πr2x/360. ∵ The complete circle is having 360 degrees & any part of it shall be equal to x/360
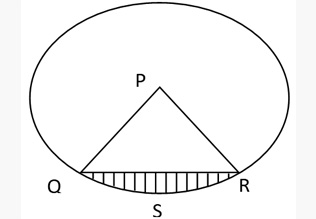
- Area of the segment of a circle (QSR) = r2[(πθ / 360°) - (sinθ / 2)]
Perimeter of the segment = 2πr(θ / 360°) + 2rsin(θ/2)















 ∠AP1B > 90° & ∠AP2B < 90°
∠AP1B > 90° & ∠AP2B < 90°











