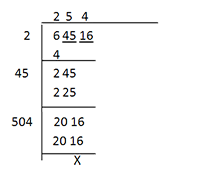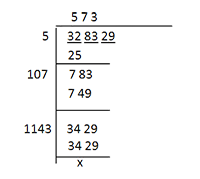To find the square root of a number, there are two methods available. First method is prime factorization and the second is the conventional square root method. Factorization is suitable only, when the numbers are relatively small and their factors can be easily found. Considering the kind of questions which appear in the competitive exams, firstly we are going to learn the conventional square root calculation method. In this, firstly the number is divided into pairs from the right hand side. If in the beginning there is a pair, then the starting is done with that pair, and if there is a single digit-number, then that would be the starting point.
Example 1: Find the square root of 64516.
Sol:
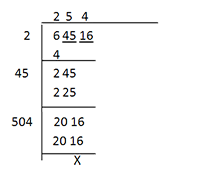
In the first place, when 6 is the single number left, after making pairs from the RHS, then you should take a number, which can be multiplied by the same number itself, and the result is less than equal to 6, which is 2.
After subtracting 4 from it, the new pair 45 is taken. The new number now becomes 245. The previous quotient is doubled and 4 is obtained. Then a number ‘x’ is written with 4, in such a way that the product of ‘4x’ and ‘x’ is less than or equal to 245. So value of x is 5.
The remainder in the next step is 20 and the last pair 16 is written with it.
Then the previous quotient 25 is doubled and 50 is obtained and a number ‘y’ is written with it in such a way that the product of ‘50y’ and ‘y’ is less than or equal to 2016.
When y is substituted by 4 the product is 2016.
In this way, the final quotient 254 is the square root of 64,516.
Example 2: Find the square root of 328329.
Sol:
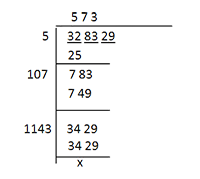
Applying the square root calculation method, in the first place after making pairs from the RHS, you are left with the number 32. Now you should take a number, which can be multiplied by the same number itself, and the result is less than equal to 32, which is 5.
After subtracting 25 from it, the new pair 83 is taken. The number now becomes 783. The previous quotient is doubled and 10 is obtained. Then a number ‘x’ is written with 10, in such a way that the product of ‘10x’ and ‘x’ is less than or equal to 783. So value of x is 7.
The remainder in the next step is 34 and the last pair 29 is written with it.
Then the previous quotient 57 is doubled and 114 is obtained and a number ‘y’ is written with it in such a way that the product of ‘114y’ and ‘y’ is less than or equal to 3429.
When y is substituted by 3 the product is 3429.
In this way, the final quotient 573 is the square root of 328,329.
Must Read Square Root Articles
Example 3: Find the smallest number with which 60 should be multiplied, so that it becomes a perfect square.
Sol: In order to answer such questions, firstly the prime factorization of the number is done. The factors of 60 are 2 × 2 × 3 × 5.
In this it can be seen that ‘2’ is occurring twice, but 3 and 5 are occurring only once. In order to make a number a perfect square every prime factor should be there twice or an even number of times. So a ‘5’ and ‘3’ is required, the product of which is 15. Therefore 15 is the smallest number.
Example 4: In a class, each of the students contributed as many paise as there are number of students. If the total collection was Rs. 144, what is the number of students in the class?
Sol: Let the number of students in the class be x. Now each of these students contributed ‘x’ paise each. So the total collection will be x2 paise. Now the total collection is given to be Rs. 144, which is 14400 paise.
As per the statement of the question x2 = 14400 Þ x = 120. Thus there are 120 students.
Note: No perfect square ends with 2, 3, 7, 8, and odd number of zeroes i.e. any number, which has 2, 3, 7 and 8 at its unit’s place and any number ending with odd number of zeroes can never be a perfect square.