Geometry plays a very important role when it comes to the preparation of competitive examinations. The questions on geometry are asked in various competitive exams. One important area of the geometry is similar triangles. In this article you are going to learn about the basics of similar triangles and its applications in some advanced questions.
What are similar triangles?
- Similar triangles are those triangles which have same shape. The size of the triangles may or may not be equal. Every pair of congruent triangles is also definitely similar to each other.
- Check for similar triangles: It is very important in geometry that you know how to check whether the given triangles are similar or not. A lot of questions which seem difficult can be solved by using the similarity of the triangles. Some questions would really become very easy, after applying the concept of similar triangles.
Similar Triangles properties
Tests for similarity:
Following are the similarity tests which can be used to check the similarity of the triangles.
1.
SSS Similarity: When the sides of one triangle are in proportion to the sides of the other triangle, then the triangles are similar. Let the triangles be ∆ABC and ∆DEF.
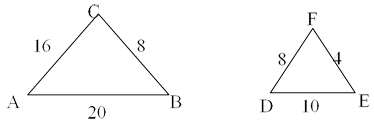
Here

It is important to note that sides opposite to equal angles are in proportion. It means that in above triangles ∠B = ∠E, ∠C = ∠F and ∠A = ∠D.
2. SAS Similarity: If two sides of a triangle are in proportion and the angles between these two sides are equal, then the triangles are similar.
3. AAA Similarity: If the angles of one triangle are equal to the angles of the other triangle, then the triangles are similar triangles.
Now we will discuss an example which can be solved by using the similarity of the triangles.
Example: In ∠ ABC, ∠ B = 90°. □ PQRS is a square of side 5 units and □ WJYZ is a square of side 10 units. MS and SY are the length and breadth respectively of rectangle MNSY. What is the length of MS?

Solution: Here ∆ ABC is a right-angled triangle. ∠ ABC = 90°.
Let ∠ BAC = Θ and ∠ BCA = 90° - Θ. As PQRS and WJYZ are squares, so ∠ MPQ = Θ and∠ PMQ = 90° - Θ. Again ∠ NJW = 90° - Θ and ∠ WNJ = Θ. Let MS = NY = x. So MQ = x - 5 and NW = x - 10. In triangles ∆MQP and ∆NWJ, ∠ PMQ = ∠ NJW,∠ MPQ = ∠ WNJ and ∠ MQP = ∠ NWJ. Hence the angles of the two triangles are equal. So ∆MQP and ∆NWJ are similar triangles and in the similar triangles the sides opposite to equal angles are in proportion.Hence we have
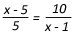
=> (x - 5) (x - 10) = 50=> x
2 - 15x + 50 = 50=> x
2 - 15x = 0=> x (x - 15) = 0=> x = 0 or 15. As x is a length, so x =
MS = 15 units
Watch Video
Similar triangles: Key Learning
- The above example is solved by using the basic result of the similar triangles. This question can also be solved by other methods but by using the similarity it becomes a simple problem. The only thing required from your side is some basic knowledge of angles such as which two angles will be equal when we have a pair of parallel lines and a transversal.
If you have any queries related to the topic, feel free to express them in the comment section below.


 It is important to note that sides opposite to equal angles are in proportion. It means that in above triangles ∠B = ∠E, ∠C = ∠F and ∠A = ∠D.
It is important to note that sides opposite to equal angles are in proportion. It means that in above triangles ∠B = ∠E, ∠C = ∠F and ∠A = ∠D.

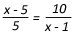 => (x - 5) (x - 10) = 50=> x2 - 15x + 50 = 50=> x2 - 15x = 0=> x (x - 15) = 0=> x = 0 or 15. As x is a length, so x =MS = 15 units
=> (x - 5) (x - 10) = 50=> x2 - 15x + 50 = 50=> x2 - 15x = 0=> x (x - 15) = 0=> x = 0 or 15. As x is a length, so x =MS = 15 units