In this article, we are going to discuss the concept of clocks. Usually, three types of questions are asked from this topic:
Type 1: Finding the time when the angle between the two hands is given.
Type 2: Finding the angle between the 2 hands at a given time.
Type 3: Questions on clocks gaining/losing time.
We will cover the first two types in this article.
Basic Concept of Clocks:
A clock is a complete circle having 360 degrees. It is divided into 12 equal parts i.e. each part is 360/12 = 30°.
As the minute hand takes a complete round in one hour, it covers 360° in 60 minutes.
In 1 minute it covers 360/60 = 6°/ minute.
Also, as the hour hand covers just one part out of the given 12 parts in one hour. This implies it covers 30° in 60 minutes i.e. ½° per minute.
This implies that the relative speed of the minute hand is 6 - ½ = 5 ½ degrees.
We will use the concept of relative speed and relative distance while solving problems on clocks.
Some facts about clocks:
- Every hour, both the hands coincide once. In 12 hours, they will coincide 11 times. It happens due to only one such incident between 12 and 1'o clock.
- The hands are in the same straight line when they are coincident or opposite to each other.
- When the two hands are at a right angle, they are 15-minute spaces apart. In one hour, they will form two right angles and in 12 hours there are only 22 right angles. It happens due to right angles formed by the minute and hour hand at 3’o clock and 9'o clock.
- When the hands are in opposite directions, they are 30-minute spaces apart.
- If both the hour hand and minute hand move at their normal speeds, then both the hands meet after 65
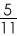 minutes.
minutes.
Now, let's apply the above concept to some questions.
Type 1: Finding the time when the angle between the two hands is given.
Solved Examples
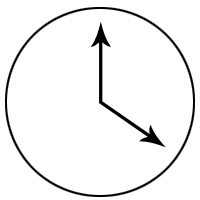
Example 1: At what time between 4 and 5, will the hands of a clock coincide?
Sol: At 4 O'clock, the hour hand has covered (4*30°) = 120°.
To catch up with the hour hand, the minute hand has to cover a relative distance of 120°, at a relative speed of 5
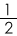
° per minute.
Thus, time required =
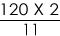
=
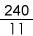
= or 21
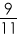
minutes.
Example 2: At what time between 10 and 11 will the minute and hour hand be at right angles?
Solution: At 10 O'clock, the hour hand has covered (10*30°) = 300°.
Note: There will be two right angles (clockwise and anti-clockwise)
Considering that hour hand is at 10, to make a 90-degree angle with the hour hand, the minute hand has to be at 1 or 7.
For the first right angle, minute hand has to cover a relative distance of (1*30) = 30°.
For the 2nd right angle, minute hand has to cover a relative distance of (7*30)= 210°.
We know that the relative speed between the two hands is of 5
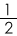
° per minute.
Hence, time required for the 1
st right angle =
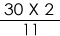
=
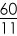
or 5
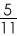
minutes.
Time required for the 2
nd right angle =
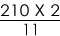
=
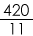
= 38
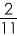
minutes.
Type 2 : Finding the angle between the two hands at a given time.
Solved Examples
Example 1: The angle between the minute hand and the hour hand of a clock when the time is 4:20 is:
Solution: At 4:00, hour hand was at 120 degrees.
Using the concept of relative distance, the minute hand will cover =
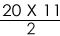
=110 degrees
The angle between the hour hand and minute hand is = 120-110 = 10 degrees.
Example 2: The angle between the minute hand and the hour hand of a clock when the time is 3:30 is:
Solution:At 4:00, hour hand was at 90 degrees.
Using the concept of relative distance, the minute hand will cover =
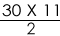
=165 degrees
The angle between the hour hand and minute hand is = 165-90= 75 degrees.
To learn the tricks to solve the third type of questions asked from this topic, read our article on Clocks-Gaining/Losing of Time.
Watch Video
Key Learning:
- Speed of the minute hand= 6° per minute.
- Speed of the hour hand= 0.5° per minute.
- The concept of relative speed is used to solve the questions on clocks. The relative speed of minute hand w.r.t hour hand=5.5° per minute.
For doubts, post your comments below and our experts will provide you with the solutions.
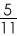 minutes.
minutes.
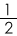 ° per minute.
° per minute.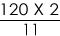 =
= 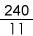 = or 21
= or 21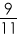 minutes.
minutes.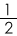 ° per minute.
° per minute.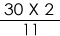 =
= 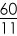 or 5
or 5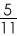 minutes.
minutes.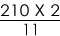 =
= 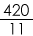 = 38
= 38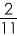 minutes.
minutes.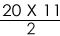 =110 degrees
=110 degrees 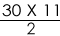 =165 degrees
=165 degrees