Percentage is a favourite topic of examiners across competitive examinations. Most students skip statement-based questions on Percentages and fractions because they appear to be lengthy and time-consuming. However, a good hold on decimals, fractions and percentages provide you an extra edge over other candidates.
So, the increased price per kg is 90/6 = Rs. 15 per kg
Learning
- This question can be solved by forming equations and then solving for price and quantity. However, a careful analysis of the statement using the concept of percentage equips you to solve the problem in a fraction of seconds!
Example 2: The difference between the marked price and the selling price on an item is same as the difference between the cost price and the selling price. Find the profit percent if the discount of
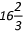
% is offered on the item.
Solution: The statement can be written in the equation form as,
Marked price - Selling price = Selling Price - Cost Price. Let us call this Equation (1). Now,
the discount offered is 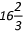 % which is nothing but 1/6 in fraction form
% which is nothing but 1/6 in fraction form. We know, Discount = Marked price - Selling Price. So, if the marked price is Rs. 6, then the Selling Price is Rs. 5. In that case, Cost Price will be equal to Rs. 4 according to equation (1). Hence, the profit percentage = Cost price - Selling price/ Cost price × 100. Substituting the values, profit percentage = ¼ × 100 = 25%.
Learning
- In most of the questions, assuming a value for the unknown and then solving the equation can prove to be the real catch. In this question, since, the denominator is 6, marked price should essentially be taken as a multiple of 6. In other cases, using 100 as the value of the unknown can easily crack the problem.
Example 3: Let A & B be two spheres such that the surface area of B is 300% greater than that of A. The volume of A is found to be k% lower than that of B, find the value of k.
- 85.5
- 92.5
- 87.5
- 90.5
Solution: Surface area of B = Surface area of A + 3(100%) Surface area of A
Which implies, Surface area of B = 4 Surface area of A (Equation 1)We know, Surface area of sphere = 4πr
2 & the volume of the sphere = 4/3 πr
3So, with respect to A and B,S
a: S
b = 1:4r
a: r
b = 1:2V
a: V
b= 1:8. Therefore, 1 - (V
a /V
b) = 7/8. According to the question, V
a = kV
b. Hence,
k= 7/8 = 87.5%. Thus, option C is the correct answer.
Learning
This is an actual exam question. A combined application of Geometry and percentage change is favourite among examiners.
The key in such questions is
- To be aware of the formula of the Surface area and Volume for various figures viz. Sphere, hemisphere, cone, cuboid, etc.
- Be careful of the squaring or cubing of the change term. Most of the students commit a mistake in this step in a hurry to solve the question
Watch Video
Percentage: Key Learnings
- While some questions require you to assume values and then solve equations, a number of questions across competitive exams are easier when solved using direct substitution of options.
- Be thorough with fractions and percentage conversions.
- It is imperative to read through the questions carefully in the exam before attempting to solve them. A cursory glance of the questions will enable you to form your strategy to crack the problem.
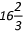 % is offered on the item.
% is offered on the item.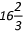 % which is nothing but 1/6 in fraction form. We know, Discount = Marked price - Selling Price. So, if the marked price is Rs. 6, then the Selling Price is Rs. 5. In that case, Cost Price will be equal to Rs. 4 according to equation (1). Hence, the profit percentage = Cost price - Selling price/ Cost price × 100. Substituting the values, profit percentage = ¼ × 100 = 25%.
% which is nothing but 1/6 in fraction form. We know, Discount = Marked price - Selling Price. So, if the marked price is Rs. 6, then the Selling Price is Rs. 5. In that case, Cost Price will be equal to Rs. 4 according to equation (1). Hence, the profit percentage = Cost price - Selling price/ Cost price × 100. Substituting the values, profit percentage = ¼ × 100 = 25%.