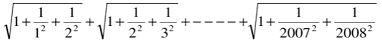In this article, we will cover the basic concepts and the approach to solve questions on Functions. We will explain two basic type of functions, Greatest Integer function and Square Root function, the most frequently asked topics across competitive exams. With specific illustrations on each function, we will also discuss a combined application of the two types.
What is Square Root function?
The principal Square Root function f(x) = √x (usually just referred to as the "square root function") is a function that maps the set of non-negative real numbers onto itself. Mathematically, √x = x ½
Properties of Square Root function
- For all real numbers x, √x2= x if x is positive or equal to 0 -x if x is negative
- For all non-negative real numbers x and y, √xy = √x√y
Example 1: Solve
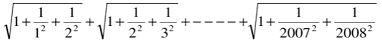
- 2008 -(1/2008)
- 2007 -(1/2007)
- 2008 -(1/2007)
- 2007 -(1/2008)
Solution: The total number of terms being added is 2007, as can be seen by the second term's denominator of each square root term.
- Let us solve this problem for all terms=n, for generalization The options can be re-written as:
- N + 1 - (1/N+1)
- N-(1/N)
- N + 1 - (1/N)
- N-(1/N+1)
- For N=1, The first term in the series comes out to be √1+(1/12 +1/22) = √9/4 = 3/2 which is nothing but S1, sum of the first term.
- Let us solve this problem by option matching and elimination. When n=1, the first option comes out to be 3/2, which is equal to S1. However, there is a possibility that other options can also yield the same answer, hence we need to check all the answers. The second option for n=1, comes out to be 0, hence, option 2 is ruled out. The third option comes out be 1, hence it can also be ruled out. The last option comes out to be ½, hence eliminated. Hence, first option is the correct answer.
Learning
- If using this approach, you are confused between two options, then increase the value of n for the remaining options after elimination. That is, suppose in this question, option 1, and option 3 yielded 3/2. Then you should check options 1 and 3, taking n=2, 3 and so on.
Measure your progress in Square root functions, take this test now.
What is Greatest Integer function?
The Greatest Integer function, also called the GINT function or Floor function is mathematically written as [x], where,
[x] = the greatest integer less than or equal to x Example, [3.4] = 3 as integers less than 3.4 are 3, 2, 1, 0.... and the greatest among these is 3. Similarly [- 5.4] = - 6 and [7] = 7.
Properties of floor function
- The floor function satisfies the identity [x + n] = [x] + n, where n is any integer. e.g. [7.6 + 8] = [15.6] = 15 and [7.6] + 8 = 7 + 8 = 15 Hence, [7.6 + 8] = [7.6] + 8
- When the interval is of the form [n, n + 1), where n is an integer, the value of the greatest integer function is n. e.g. The value of the greatest integer function is 5 in the interval [5, 6)
Solved examples on Greatest Integer function
Example 2: Which of the following cannot be the value of [ 3√1 ] + [ 3√2 ] + [ 3√3 ] + ........+ [ 3√n > ] ?
- 37
- 188
- 190
- 153
Solution: Breaking the problem into steps,
- The value of [ 3√1 ] is 1 and it will remain 1 till [ 3√7 ] as cube of 2 is 8, so [ 3√8 ] = 2. Hence, the sum of first 7 terms is 7.
- The values of each term from [ 3√8 ] to [ 3√26 ] is 2. The sum of these 19 terms is 38. The sum of all the 26 terms will be 7 + 38 = 45.
- It also implies that for 7 < n < 27, the sum of these terms will be 7 + 2k. That means the sum 37, which is of this form only is definitely possible. So, the first option is possible.
- From [ 3√27 ] to [ 3√63 ], each of the 37 terms has value 3 and their total will be 111. Now total up to this point is 156. Hence, 153 is also possible.
- Now, [ 3√64 ] = 4 and the value of next 61 terms will be 4 each. That also means the sum for n > 63 will be 156 + 4k.
Now, 188 is a number of this form and is possible and 190 is not possible as it cannot be written in the form of 156 + 4k. Hence, we have successfully identified the answer.
Let us solve a question on the combined application of Square root function and GINT function. Such types of combined questions appear frequently across competitive examinations.
Practice the actual exam questions and take your preparation to the next level.
Example 3: Find the value of [√1 ] + [√2 ] + [√3 ] + [√4 ] + ..... + [√24 ], where [x] is the greatest integer less than or equal to x.
Solution: Here from [ √1 ] to [ √3 ] each term has value 1, as the square root of all these numbers will be greater than equal to 1 but less than 2. The greatest integer less than those will be 1. So, the total of these three terms will be 3.
- The value of each term from [ √4 ] to [ √8 ] is 2 on the base of the same logic as explained above, so the total of these 5 terms is 10.
- From [√9 ] to [ √15], the value of each term is 3 and total of these 7 terms is 21.
- Similarly, the value of each term from [ √16 ] to [ √24 ] is 4 and the sum of these 9 terms is 36.
So, we have [√1 ] + [√2 ] + [√3 ] + [√4 ] + ..... + [√24 ] =
3 + 10 + 21 + 36 = 70.
Math Functions: Key Learnings
- Usually, questions based on Square root and GINT can be cracked with the help of option matching and elimination.
- Most competitive examination test your ability to apply basic properties of functions in questions, therefore, a thorough understanding of the same is immensely helpful.
In case of any query regarding any illustration or concept mentioned, ask questions! Write to us in the comment section below.