In this article, you will learn a quick approach to tackle remainder based questions in Number system. Let's start with an example:
The apparent complexity of this question can send a chill down the spine of students. However, one concept that makes such questions very simple and easy, is the concept of Euler number.
The Euler number of a number x means the number of natural numbers which are less than x and are co-prime to x. E.g. the Euler number of 6 will be 2 as the natural numbers 1 & 5 are the only two numbers which are less than 6 and are also co-prime to 6.
So, the Euler number of 20 will be
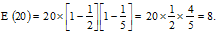
Hence, there are 8 numbers less than 20, which are co-prime to it.
Cross check: Numbers co-prime to 20 are 1, 3, 7, 9, 11, 13, 17 and 19, 8 in number.
Application of Euler's Theorem:
- This concept has a wonderful application in answering remainder questions.
- When yE (z) is divided by z, the remainder will always be 1 Where, E(z) is Euler number of z and y and z are co-prime to each other.
- When yE (z).k is divided by z, where k is an integer, remainder will always be 1 That is if the power is any multiple of the Euler number of the divisor, even in that case the remainder will be 1.
Take this test now to assess your understanding of Euler number.
Example 2: What is the remainder when 1318 is divided by 19?
Solution: If yE (z) is divided by z, the remainder will always be 1; if y, z are co-prime In this case the Euler number of 19 is 18
(The
Euler number of a prime number is always 1 less than the number). As 13 and 19 are co-prime to each other,
the remainder will be 1.
Example 3: What is the remainder when 1332 is divided by 15?
Solution: Now in this case the Euler number of 15 is 8
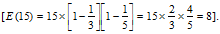
Now the Numerator can also be written as 13
8×4. Thus the remainder in this case will be 1.
Must Read Number System Articles
- Number System - Euler's theorem to find Remainder
Example 4: Now, let us solve the question given at the beginning of the article using the concept of Euler Number:
What is the remainder of 19
2200002/23?
Solution: The Euler Number of the divisor i.e. 23 is 22, where 19 and 23 are co-prime.
- Hence, the remainder will be 1 for any power which is of the form of 220000.
- The given power is 2200002. Dividing that power by 22, the remaining power will be 2.
- Your job remains to find the remainder of 192/23. As you know the square of 19, just divide 361 by 23 and get the remainder as 16.
Example 5: How many numbers from 1 to 300 can neither be divisible by 2, nor by 3 nor by 5?
Solution: The Euler number of 300 is 80, which is the answer.
How ready are you now in Number System? Take this test and get the answer.
Watch this Achievers video on Euler's theorem to grasp all tips & tricks to ace the exam.
Key Learning:
- Euler's theorem is the most effective tool to solve remainder questions.
- As seen in Example 5, Euler's theorem can also be used to solve questions which, if solved by Venn diagram, can prove to be lengthy.
where P, Q and R are the different prime factors of z.
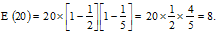Hence, there are 8 numbers less than 20, which are co-prime to it. Cross check: Numbers co-prime to 20 are 1, 3, 7, 9, 11, 13, 17 and 19, 8 in number.
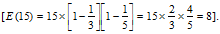Now the Numerator can also be written as 138×4. Thus the remainder in this case will be 1.
-icon.jpg?null&itok=2FjKP8-O "Chain Rule Practice Problems"){kind=icon}
