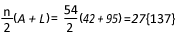In this article, we are going to discuss the concept of Digital Root (DR) also known as seed number. This concept is a very powerful tool for saving time and effort in certain long calculations questions both in quant section as well as in data interpretation.
What is Digital Root?
Now, let us understand the concept of Digital Root/ Seed number in detail. Digital Root is the single number obtained by adding the number successively. E.g. Digital Root of 347 = 3 + 4 + 7 = 14, 14 = 1 + 4 = 5. Thus, 5 is a single digit number, which is the digital root/ seed number of 347.
Properties of Digital Root
Some of the important and useful properties of digital root are:
- When you multiply any number by 9, the digital root will always be 9. E.g. 7 X 9 = 63. 6 + 3 = 913 X 9 = 117. 1 + 1 + 7 = 924 X 9 = 216, 2 + 1 + 6 = 9 and so on.
- When we add 9 to a number, it does not change the digital root of that number. E.g. 417 = 4+1+7= 12, 1+2 = 3. Now, if we annex 9 to this number i.e. 4179 = 4+1+7+9 = 21, 2+1 = 3. Hence, we observe that adding 9 does not change the DR of that number. So, we can omit 9 while calculating the digital root of a number and we can also omit any 2 or more numbers which add to 9 and still get the same digital root. This property eases out to calculate digital roots of certain numbers.e.g. = 97 = 9 + 7 = 16, 1 + 6 = 7 so even if we omit 9 still DR is 7.
- When we divide any number by 9, the digital root of that number will be the remainder. E.g.
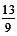 remainder is 4 which is same as digital root of 13 (1 + 3 = 4)
remainder is 4 which is same as digital root of 13 (1 + 3 = 4)  remainder is 2 which is again same as 4 + 7 = 11, 1 + 1 = 2.
remainder is 2 which is again same as 4 + 7 = 11, 1 + 1 = 2.
- Digital root of any number will be from 1 to 9. As by definition only digital root of a number is obtained after adding the digits of a number successively until one gets the single digit.
- Digital root of any perfect square will fall among 1, 4, 7, 9 onlye.g. 16 = 1 + 6 = 736 = 3 + 6 = 949 = 4 + 9 = 13, 1 + 3 = 464 = 6 + 4 = 10, 1 + 0 = 1 and so on.
Solved Digital Root Problems
Example 1: 3286 x 4783 = 1. 15766938 2. 16716938 3. 15716938 4. 17716948
Solution: Now let us apply digital root technique instead of solving it conventionally.
DR of 3286 = 1 and 4783 = 4. Now, since these two numbers were to be multiplied so let us multiply their DRs i.e. 4 x 1 = 4.Hence, the DR of actual product of these numbers has to be 4 and only 3rd option i.e.
15716938 has DR = 4.
Example 2: S (x) = Sum of all the digits of natural number x. e.g. S(245) = 2 + 4 + 5 = 11
Find the value of V. Where V = [S (42) + S (43) + S (44) + .... + S(95)]1. 4842. 5853. 474. 485
Solution: Conventional Approach: At the ten's place 4 will come 8 times only but 5, 6, 7 & 8 each will come 10 times and finally 9 will come 6 times. So the total at ten's place [(4 × 8) + (5 + 6 + 7 + 8) 10 + (9 × 6)] = 346 At the units place all the ten digits (from 42 to 51) including zero will come 5 times and then we also include units places of (92 to 95), the total at units place = 5 × (∑ 9) + 14 = 225 + 14 = 239. Now, value of V = 346 + 239 = 585
Digital Root Method
- Using this approach we can simply take the sum of the series as an arithmetic progression with 42 as first term 'A', 95 as last term 'L' and common difference being 1. The number of terms 'n' will be (95 - 42 + 1) = 54.
Now using the formula for summation of A.P. - Sn =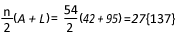
- Now calculating DR of 27 = 2 + 7 = 9, we need not calculate anything further as we already know that any number, when multiplied by 9, gives a DR of 9 only. So, the answer to this calculation will have the DR = 9.
- Now we can simply check through the choice that which choice has DR = 9. This is true only for 2nd choice i.e. 585. So we observed how simple the calculation become using the digital root approach.
Watch Video
Number System- Digital Root: Key Learning
- Lengthy Calculations are required in various competitive exams. In this article, we are able to understand the concept of digital root and its application as a shortcut approach to solve typical Quant questions.
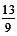 remainder is 4 which is same as digital root of 13 (1 + 3 = 4)
remainder is 4 which is same as digital root of 13 (1 + 3 = 4) 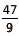 remainder is 2 which is again same as 4 + 7 = 11, 1 + 1 = 2.
remainder is 2 which is again same as 4 + 7 = 11, 1 + 1 = 2.