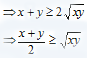Algebra forms an integral part of Quant section of various competitive examinations. Within algebra, a very important area from examination point of view is Progressions i.e. Arithmetic progression (A.P.) and Geometric Progression (G.P.). In this article, we will discuss mainly about Arithmetic mean (A.M.) and Geometric Mean (G.M.) as a lot of questions are asked from these two areas.
Arithmetic Progression
- Three numbers a, b & c are said to be in Arithmetic progression if b - a = c - b i.e. if the difference between the terms is same. This difference between the terms is called the common difference
- Eg. 5, 9, 13, 17, 21.... is an Arithmetic progression as the difference between the terms is same.
Arithmetic Mean definition and Formula
- As b - a = c - b => 2b = a + c or
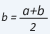 . Here 'b' is called the Arithmetic mean between 'a' and 'c'. In general, Arithmetic mean of the 'n' terms is equal to their average.
. Here 'b' is called the Arithmetic mean between 'a' and 'c'. In general, Arithmetic mean of the 'n' terms is equal to their average.
Geometric Progression
- Three numbers a, b and c are said to be in Geometric progression if
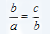 i.e. if the ratio of the terms is same. This ratio of the terms is called the common ratio.
i.e. if the ratio of the terms is same. This ratio of the terms is called the common ratio.
- Eg. 4, 16, 64, 256, 1024….. is a Geometric progression as the ratio of the terms is same.
Geometric Mean definition and Formula
- As
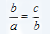 => b2 = ac or
=> b2 = ac or 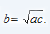 . Here 'b' is called the Geometric mean between 'a' and 'c'. In general, the geometric mean of 'n' numbers x1, x2, x3,.....xn is given by
. Here 'b' is called the Geometric mean between 'a' and 'c'. In general, the geometric mean of 'n' numbers x1, x2, x3,.....xn is given by 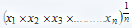
Take this test now to assess your understanding of the topic.
Relation between Arithmetic Mean and Geometric mean:
- The relation between Arithmetic mean and Geometric mean is very important. A lot of questions are asked based on this relation only.
Let us check the relation between the two.
- Let x and y are two positive real numbers. Then we have (x - y)2 = 0
=> x2 +y2 - 2xy = 0
=> x2 +y2 - 2xy +4xy - 4xy = 0
=> x2 +y2 + 2xy - 4xy = 0
=> x2 +y2 + 2xy = 4xy
=> (x + y)2 = 4xy
Hence for any positive real numbers A.M. = G.M. This is an important result and questions are frequently asked based on this result. Let us take an example
Example 1: Find the maximum value of ab (72 - 3a - 4b), for a, b > 0.
Solution: Now in this question, you have to find the maximum value. As 'a' and 'b' are positive real numbers, so it is not possible to find the maximum value by putting random values for 'a' and 'b'. Now here comes the role of the above result.
As we know A.M. = G.M.
We will apply the above result on three numbers 3a, 4b and (72 - 3a - 4b). We have selected these numbers as there sum will be a constant number and their product will have the terms required in the question.
Hence the maximum value of ab(72 - 3a - 4b) is 1152.
Measure your progress in A.M. and G.M. by taking this test now.
Cover all the concepts of Progressions - Arithmetic mean and Geometric mean in one go by watching this video
Progressions: Key Learnings
- This concept is useful when we have to find the minimum and maximum values of the expressions and we cannot do that by substituting the random values for the variables.
- As it is seen from the above example that if you put different values of 'a' and 'b' in the given expression then you will get different values and you cannot say which one is the maximum but by going through the result the maximum or the minimum value can be easily found. After solving a reasonable number of questions based on this, you will learn to take the appropriate values to get the desired answer.
If you have any queries related to Algebra Progressions, feel free to post them in the comments section below.
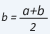 . Here 'b' is called the Arithmetic mean between 'a' and 'c'. In general, Arithmetic mean of the 'n' terms is equal to their average.
. Here 'b' is called the Arithmetic mean between 'a' and 'c'. In general, Arithmetic mean of the 'n' terms is equal to their average.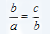 i.e. if the ratio of the terms is same. This ratio of the terms is called the common ratio.
i.e. if the ratio of the terms is same. This ratio of the terms is called the common ratio.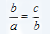 => b2 = ac or
=> b2 = ac or 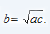 . Here 'b' is called the Geometric mean between 'a' and 'c'. In general, the geometric mean of 'n' numbers x1, x2, x3,.....xn is given by
. Here 'b' is called the Geometric mean between 'a' and 'c'. In general, the geometric mean of 'n' numbers x1, x2, x3,.....xn is given by