In this article, we are going to learn the concept of cube cutting or cutting the painted cube. While solving these questions, the most important part is to visualise the cube. Cube cutting is an important concept as questions are frequently asked from this topic in a number of competitive exams.
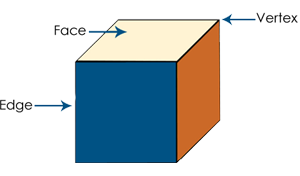
Let's first learn some basic terminologies i.e. face, vertex and edge of a cube.
In a cube, there are 6 faces, 8 vertices & 12 edges. Vertex means corners & edge means side.
Generally, questions from this topic are of the type wherein, a cube with side measuring unit 'x' is painted on all faces and is cut into smaller cubes with sides measuring unit 'y'. You are then required to find the number of cubes having 'n' faces painted.
The first thing that you need to figure out is the number of smaller cubes. For this, you look at one particular edge of the big cube and figure out how many smaller cubes can fit into this. It will be x/y. So, the number of smaller cubes will be (x/y)3.
Since all the smaller cubes will have at least one face facing inside i.e. not on the surface of the original cube, hence, none of the smaller cubes will have all faces painted. Further, since the maximum number of faces of the larger cube that intersect at a point are 3(at the corners), hence, the smaller cubes can have a maximum of 3 faces painted.
So, the number of smaller cubes with 3 faces painted = No of corners of larger cube = 8 (always), provided none of the faces of the larger cube is left unpainted.

Let us apply this theory to the given questions.
Cube Cutting Sample Questions
Example 1: A cube having a side of 6 cm is painted red on all the faces and then cut into smaller cubes of 1 cm each. Find the total number of smaller cubes so obtained.
Solution:

As explained above, the number of smaller cubes = (6/1)3 = 216 smaller cubes.
(Here x=6 and y=1)
Example 2: In the above example, how many cubes will have three faces painted?
Solution: As explained above, only the corner cubes i.e. the 8 cubes at the corners of the original cube will have three faces painted. Hence the answer will be 8 only.
To find the number of smaller cubes with only 2 faces painted, you need to consider the cubes where 2 faces of the bigger cube meet, i.e. the edges. Remember, this includes the cubes present at the corners as well, so you need to remove those 2 cubes from the number of cubes on each edge.
Example 3: In the above example, how many cubes will have only two faces painted?
Solution: As discussed above, only the cubes at the edge of the bigger cube can have two faces painted.
The larger cube has 6 cm edge and smaller cube is 1 cm edge. Hence, there are 6 cubes on each edge. However, you need to consider 4 middle cubes only, as the 2 cubes on each corner will have 3 painted faces.
Hence, there are 4 such cubes on each edge. As there are 12 edges, there will be 4*12 = 48 cubes
.
Example 4: In the above example, how many cubes will have only one face and no side painted?
Solution: As discussed above, only the cubes at the face of the bigger cube can have only one painted face. Since the larger cube has 6 cm edge and smaller cube is 1 cm edge, hence, if you see one of the faces of the larger cube, you will see 6*6 = 36 cubes. Out of these, exclude the cubes which lie on the edges, as they have two or more faces which are painted. Thus, on each face of the original cube, there will be 4*4 = 16 cubes will have only one face painted.
As there are 6 such faces, the number of such smaller cubes will be 16*6 = 96.
Lastly, the number of cubes having no faces painted can be found by subtracting the sum of the painted cubes from the total number of smaller cubes. Therefore, the required answer is 216 – (8 + 48 + 96) = 64 cubes.
Example 5: A cube having an edge of 12 cm each. It is painted red on two opposite faces, blue on one other pair of opposite faces, black on one more face and one face is left unpainted. Then it is cut into smaller cubes of 1 cm each. Answer the following questions:
- The number of smaller cubes which are having three-faces painted.
- The number of smaller cubes which are having two-faces painted.
- The number of smaller cubes which are having one-face painted.
- The number of smaller cubes which are having zero-face painted.
Solution:

- Total number of cubes= (12*12*12)/(1*1*1)=1728
- For a cube with all sides painted we have 8 cubes with 3 sides colored. But here we have 1 side unpainted. Therefore, we will have only 4 cubes with 3 sides painted. The other 4 cubes will have only 2 sides painted.
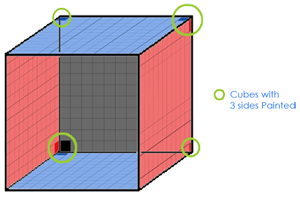
- For 2 sides painted, we look for the edges.
A cube has 12 edges.
8 edges, each edge having 10 cubes will have 2 sides painted. (4 edges of an unpainted side won’t be included).
We'll also include those 4 cubes (which we didn’t count while counting 3 coloured sides, as they have 2 sides painted)
Cubes on 4 edges of the unpainted side of the cube will have 1 side painted (due to the unpainted side).
Therefore, total cubes with 2 sides painted= 8*10 + 4= 84 cubes.
- For 1 side painted, we look for the faces of the cube.
A cube has 6 faces.
5 faces each having (12-2)*(12-2) = 100 cubes will have one side painted.
We’ll have to include those cubes on the edges linked with an unpainted face.
10 cubes on each of those edges will have 1 side painted.
Therefore, total cubes with 1 side painted= 5*100 + 4*10 = 540 cubes.
- According to the formula, cubes with no side painted= (12-2) 3= 1000.
But we have to include the cubes from the unpainted side too. It will be 10*10=100
So, total number of unpainted cubes= 1000+100=1100.
Shortcut Formulae
- For a cube of side n*n*n painted on all sides which is uniformly cut into smaller cubes of dimension 1*1*1,
- Number of cubes with 0 side painted= (n-2) 3
- Number of cubes with 1 sides painted =6(n - 2) 2
- Number of cubes with 2 sides painted= 12(n-2)
- Number of cubes with 3 sides painted= 8(always)
- For a cuboid of dimension a*b*c painted on all sides which is cut into smaller cubes of dimension 1*1*1,
- Number of cubes with 0 side painted= (a-2) (b-2) (c-2)
- Number of cubes with 1 sides painted =2[(a-2) (b-2) + (b-2)(c-2) + (a-2)(c-2) ]
- Number of cubes with 2 sides painted= 4(a+b+c -6)
- Number of cubes with 3 sides painted= 8
Key Learning:
To summarise, the number of three faces painted cubes may be found with the help of vertices, two-faces painted with the help of edges and one-face painted with the help of faces. By using this learning, we can even solve complex questions on cube cutting for example cube painted with different colours.




