Directions: Concepts Explained with examples

In this article, we are going to discuss how to solve direction sense test questions in reasoning. Questions based on this concept are frequently asked in various aptitude tests and competitive exams. Directions questions asked in the exam are based on two principles-

The first step for solving the questions using the concept of 'directions' is to understand the direction chart, which has 8 directions. Take a look at the direction chart given below.

The first point you need to remember is that each main direction change undergoes a 90° change in direction e.g. from North to West/East it will be 90° change. But the change between North and North-east is only 45°.

The next important point that needs to be kept in mind is that directions problems generally quiz you about the minimum distance, distance by air, crow fly distance etc. For the purpose of solving these questions, we assume all these distances to be along straight lines and between specified points. We use the concept of Pythagoras theorem to solve the questions. This concept is discussed in this article.

A person facing north, on taking left will face towards west and on taking the right turn towards east.

A person facing west, on taking left will face towards south and on taking right turn towards north.

A person facing east, on taking left will face towards north and on taking the right turn towards south.

A person facing south, on taking left will face towards east and on taking the right turn towards west.

Hence, we can sum up the above points as:

We'll use the concept of Pythagoras theorem to solve the questions on directions.

In a right-angled triangle, the square of the hypotenuse is equal to the sum of the squares of the other two sides.

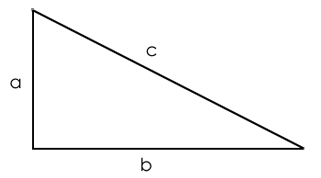
c²=a² + b²
Let's understand the above discussed concepts with the help of some solved examples.

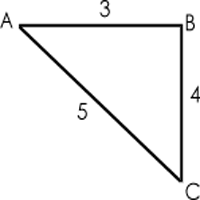
Example 1: A man goes 3 kms. East from point A and then takes a right turn from point B to move 4 kms. to point C. What is the minimum distance between point A and point C?

Solution: In order to find the minimum distance between these points, we use a little bit of geometry. We know that the minimum distance between these points will lie along the hypotenuse of the right-angled triangle formed by these points.

Now applying Pythagoras theorem, the distance between the starting point A and final point C is 5 kms i.e. the square root of the sum of squares of 3 and 4.

An important point to learn from this question could be the fact that you might be asked to specify the direction of the specific point, for example, the question might state: "in which direction is he with respect to the starting point". The answer would be South-east.

Now, in case the question was: "In which direction is the starting point with respect to C"; the answer would be North-west.

Another question could be: "In which direction is he walking towards point C"; the answer would be South.

While calculating the distance from a starting point to the destination point when the points form a right-angled triangle, the prior knowledge of Pythagorean Triplets (3-4-5, 5-12-13, 8-15-17 etc.) is generally very helpful in calculating the distances involved as it saves time spent on calculations. Let us solve an example that uses this knowledge.

Example 2: A child is looking for his father. He went 90 metres in the East before turning to his right. He went 20 meters before turning to his right again to look for his father at his uncle’s place 30 metres from this point. His father was not there. From here he went 100 metres to the North before meeting his father in a street. What is the smallest distance between the starting point and his father’s position?

The movement of the child from A to E is as shown in fig.
Clearly, the child meets his father at E.
Now, AF = (AB - FB)
= (AB - DC) = (90 - 30) m = 60 m.
EF = (DE - DF) = (DE - BC)
= (100 - 20) m = 80 m.

Now the distance is square root of (60² + 80²), which will be 100 metres.

We can clearly see from the above example that knowledge of basic concepts can go a long way in reducing the time you take to solve problems, along with improving your accuracy. Make sure you place sufficient emphasis on the topics such as 'direction based questions', and your performance is surely meant to improve.

Answer: