Q1. What will the 12th letter of the alphabet if the second half of the alphabet is written in reverse order?
Answer: Option 3
Sol:
| A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| → |
| N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
| 14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
| → |
The most essential thing to note in a question like this is to find out where exactly the required position falls, i.e. in the second half of the alphabet or the first half of the alphabet. So, the answer falls in the first half. Now, even if the second half of the alphabet is written in reverse order, it will have no effect on the position of our 12th letter. So in this particular case, we have to simply decide the 12th letter from the left hand side of the alphabet, which is L, by using the EJOTY method discussed earlier.
Q2. What will be the 11th letter from the right side if the first half of the alphabet is written in reverse order?
Answer: Option 4
Sol:
| M |
L |
K |
J |
I |
H |
G |
F |
E |
D |
C |
B |
A |
| → |
| N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
| → |
Now examine this illustration carefully. It is exactly similar to the first question that we discussed. If we want to count from the right hand side of the alphabet & the answer falls in the first half from right hand side (the actual second half of the alphabet is now the first half of the alphabet as you start counting from this side). So, reversing the first half of the alphabet of a normal alphabet will have no effect on the correct answer. So the question can be rephrased like finding the 11th letter from the right hand side of the alphabet. The correct answer as you can find is P.
Must Read Series Alphabet Articles
Q3. Which letter in the alphabet will be 16th from the left hand side if the second half of the normal alphabet is reversed?
Answer: Option 2
Sol:
| A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| → |
| Z |
Y |
X |
W |
V |
U |
T |
S |
R |
Q |
P |
O |
N |
| 14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
| → |
Your answer will fall in the second half of the alphabet (as the first half of the alphabet is complete when you are at 13th position from the left hand side of the alphabet). So the letters A to M remain the same while the letters N to Z are written from Z, Y, X till N. So, we can count 13 letters from A to M & then add three letters from the behind of the alphabet. You can see that the third letter from back side is X, which is the correct answer to the given question. So, we have solved this particular question by looking at the above alphabet. Let us solve it in a faster way without looking up the alphabet given above.
Now, since only the second half of the alphabet is to be reversed, we can easily skip the first half that is the first 13 letters of the alphabet, which should be assumed to have been counted in a completely normal way. Now, the question remains as how to find the 16
th letter from the left hand side of the alphabet with the reversed second half of the alphabet. Simply, you can count the 3rd letter from the right hand side of the alphabet (which is obviously the 24th from the left hand side of the alphabet), which if added to the number 13, makes it the 16th from the left hand side of the alphabet. Refer to the above figure for clarity. Applying the earlier process, the third letter from right hand side of the alphabet is X, so we get the same answer to the given question.
Q4. What would be the 14th letter from the left side if the normal English alphabet was written in reverse order?
1. M
2. C
3. J
4. None of these
Answer: Option 1
Sol: For better understanding of the EJOTY rule, let us write the alphabets in the reverse order.
| A |
B |
C |
D |
E |
F |
G |
H |
I |
J |
K |
L |
M |
| 1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
| → |
| 26 |
25 |
24 |
23 |
22 |
21 |
20 |
19 |
18 |
17 |
16 |
15 |
14 |
| ← |
| N |
O |
P |
Q |
R |
S |
T |
U |
V |
W |
X |
Y |
Z |
| 14 |
15 |
16 |
17 |
18 |
19 |
20 |
21 |
22 |
23 |
24 |
25 |
26 |
| → |
| 13 |
12 |
11 |
10 |
9 |
8 |
7 |
6 |
5 |
4 |
3 |
2 |
1 |
| ← |
So, the alphabet will look like Z, Y, X… from left hand side if we reverse the whole of the alphabet. Imagine that what was on the left hand side of the alphabet earlier is on the right hand side of the alphabet now. Then, A will go on the extreme right hand side, followed by B and so on. Practically, what was 14th from the left hand side of the alphabet earlier is the 14th from the right hand side of the alphabet now. So if this 14th letter from right hand side of the alphabet can be converted to left hand side of the alphabet i.e. 13 and we know from EJOTY rule that the 13th from left hand side is M.
Q5. Which is the 4th letter to the right of the 8th letter from the left side?
Answer: Option 4
Sol: We should see the latter part of the question. If we start counting from the left side, we will arrive at the 8th letter which is H. Starting from H, you have to find the 4th letter to its right, which is L. Practically, L is placed at the 12th position from the left side which you can get by adding the numbers given in the question (8+4).
Rule: Whenever you are given 2 opposite directions to count from, i.e., left- right or right-left, you should add up the 2 numerals & should count from the direction that is given at the end of the question.
Q6. BEI : NTA : : IRB : ?
1. JPW
2. PCR
3. MYL
4. SJE
Answer: Option 3
Sol:The components of all these given sequences are related to their preceding and following components in a particular manner. To ease the subject, we shall assign the respective alphabetical positions to the letters.
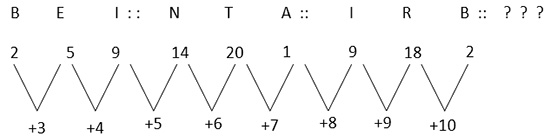
You can see in the above example that the difference between successive components is increasing by 1 position every time. This question asks you to determine the next 3 letters working with the similar logic. It is here that EJOTY formula will prove very handy. Applying that formula, you can easily find the correct answer i.e. +11, +12 and then +13, which turns out to be MYL.
Q7._xx_ yx _ yy _ xy _ xxy
1. xxxyy
2. yxyxy
3. yyxxy
4. yyyxx
Answer: Option 3
Sol:Here applying the same logic as explained above, when you fill the third option in the blanks you get yxxy/yxxy/yxxy/yxxy. This becomes a valid pattern and hence the answer is option 3.
Q8.xz _ zxy _ yxzx _ xyx _ xzxz.
1. xxzy
2. xzyz
3. yxyy
4. yzyy
Answer: Option 1
Sol:Applying the same logic as explained above, when you fill the first option in the blanks you get xzxz/xyxy/xzxz/xyxy. Thus xzxz and xyxy is repeated alternatively. Thus first option is the answer.
Q9.APZLT, BQYMR, CRXNP, DSWON, ?
1. KVIUJ
2. JUUVK
3. ETVPL
4. KUUVJ
Answer: Option 3
Sol:First letter in every group of words is in ascending order of ABCDE. The second letter in every group of words is also in the ascending order of PQRST, the third letter in every group of words is in the descending order of ZYXWV, fourth letter in every group of words is in the ascending order of LMNOP and the last letter in every group of words is in the descending order with a gap of one letter, i.e., ETVPL.
Q10.Which of the following will come in place of the question mark (?) in the following letter series?
BXF, DVI, FTL, HRO,?
1. JPL
2. KPL
3. JOL
4. None of these
Answer: Option 4
Sol:First letter moves +2 steps. Second letter moves – 2 steps. Third letter moves + 3 steps. JPR replaces the ‘?’. Hence answer is option 4.
