In the figure above, DABC is a right triangle, so (AB)2 + (AC) 2 = (BC)2. Here, AB = 6 and AC= 8, so BC= 10, since 62 + 82 = 36 + 64 = 100 = (BC) 2 and BC = &redic;100.
Must Read Triangles Articles
Any triangle in which the lengths of the sides are in the ratio 3:4 is always a right angled triangle.
In general, if x, by and z are the lengths of the sides of a triangle in which x2 + y2 = z2, then the triangle is said to be a right angled triangle.
There are some Pythagorean triplets, which are frequently used in the questions. It is better to memorize these triplets.
- 3, 4 & 5
- 5, 12 & 13
- 7, 24 & 25
- 8, 15 & 17
- 9, 40 & 41
- 11, 60 & 61
- 12, 35 & 37
- 16, 63 & 65
- 20, 21 & 29
- 28, 45 & 53.
Any multiple of these Pythagorean triplets will also be a Pythagorean triplet i.e. when we say is a 5,12, 13triplet, if we multiply all these numbers by 3, it will also be a triplet i.e. 15, 36, 39 will also be a Pythagorean triplet.
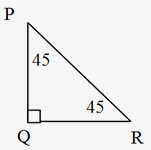
(iv) 45°- 45° - 90° Triangle: Special Triangles: If the three angles of a triangle are 45°, 45° & 90°, then the perpendicular side of that right angled triangle is 1 / &redic;2 times the hypotenuse of the triangle. In a 45°- 45°- 90° triangle, the lengths of the three sides of that triangle are in the ratio 1: 1: &redic;2.
For example, in ∆PQR, if PR = 2cm, then PQ = &redic;2cm and QR = &redic;2cm.
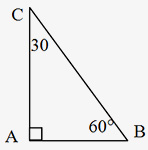
(v) 30°- 60° - 90° Triangle: In a 30°- 60° - 90° triangle, the lengths of the three sides of that triangle are in the ratio 1: &redic;3 : 2. For example, in ∆ABC, if AC = 3, then AB = 3&redic;3 and BC = 6. To summarize, the below mentioned formulae can be applied to calculate the other two sides of a 30°- 60°-90° triangle, when one of the three sides is given.
Side opposite to 30° = ½ of hypotenuse.
Side opposite to 60° = &redic;3/2 of hypotenuse.
Some important properties of triangles
(i)The sum of the three interior angles of a triangle is 180°.
In ∆ABC, ∠ABC + ∠BAC + ∠ACB = 180°
(ii)The sum of an interior angle and the adjacent exterior angle is 180°.
In figure on previous page, ∠ABC + ∠ABH = 180°
∠ABC + ∠CBI = 180°
(iii)Two exterior angles having the same vertex are congruent.
(iv)The measure of an exterior angle is equal to the sum of the measures of the two interior angles (called remote interior angles) of the triangle, not adjacent to it.
(vi)The sum of any two sides of a triangle is always greater than the third side.
In ∆ABC, AB + BC > AC, also AB + AC > BC and AC + BC > AB.
(vii)The difference of any two sides is always less than the third side.
Altitude: The altitude of a triangle is the segment drawn from a vertex perpendicular to the side opposite that vertex. Relative to that vertex and altitude, the opposite side is called the base.
The area of a triangle is equal to: (the length of the altitude) × (the length of the base) / 2.
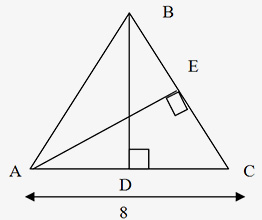
BD = 5
In ∆ABC, BD is the altitude to base AC and AE is the altitude to base BC.
Triangle Formula: The area of a triangle ∆ABC is equal to ½ × BD × AC = ½ × 5 × 8 = 20.
The triangle area is also equal to (AE × BC) / 2. If DABC above is isosceles and AB = BC, then altitude BD bisects the base; that is, AD = DC = 4. Similarly, any altitude of an equilateral triangle bisects the side to which it is drawn.
Congruency of triangles: If the sides and angles of one triangle are equal to the corresponding sides and angles of the other triangle, then the two triangles are said to be congruent.
Two triangles are congruent if
- Two sides & the included angle of a triangle are respectively equal to two sides & included angle of other triangle (SAS).
- 2 angles & 1 side of a triangle are respectively equal to two angles & the corresponding side of the other triangle (AAS).
- Three sides of a triangle are respectively congruent to three sides of the other triangle (SSS).
- 1 side & hypotenuse of a right-triangle are respectively congruent to 1 side & hypotenuse of other rt. triangle (RHS).
Similarity of triangles:
Two triangles are said to be similar to each other if they are alike only in shape. The corresponding angles of these triangles are equal but corresponding sides are only proportional. All congruent triangles are similar but all similar triangles are not necessarily congruent.
Two triangles are similar if
- Three sides of a triangle are proportional to the three sides of the other triangle (SSS).
- Two angles of a triangle are equal to the two angles of the other triangle (AA) respectively.
- Two sides of a triangle are proportional to two sides of the other triangle & the included angles are equal (SAS).
Properties of triangles:
- If two triangles are similar, ratios of sides = ratio of heights = ratio of medians = ratio of angle bisectors = ratio of inradii = ratio of circum radii.
- Ratio of areas = b1h1/b2h2 = (s1)2/(s2)2 , where b1& h1 are the base & height of first triangle and b2& h2 are the base & height of second triangle. s1& s2 are the corresponding sides of first and second triangle respectively.
- The two triangles on each side of the perpendicular drawn from the vertex of the right angle to the largest side i.e. Hypotenuse are similar to each other & also similar to the larger triangle.
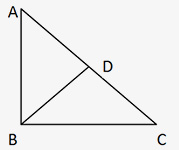
∆ DBA is similar to ∆ DCB which is similar to ∆ BCA.
- The altitude from the vertex of the right angle to the hypotenuse is the geometric mean of the segments into which the hypotenuse is divided.
i.e. (DB)2 = AD * DC
Circum center: The circum center is the center of a triangle's circum circle. It can be found by the intersection of the perpendicular bisectors.
Incenter: The incenter is a point representing the center of incircle for a polygon. The corresponding radius of the incircle is known as the inradius of the incircle.






