Venn Diagrams: Maxima and Minima - Part 1

In this article, we are going to discuss the concept of maxima and minima in Set Theory/Venn Diagrams. You will find a lot of questions related to this concept in various competitive exams. Hence, it is of paramount importance that you learn the technique to solve questions on this topic.

First, let us discuss the concept in case of 2 variables.

The best way to understand this topic is with the help of examples.

Question 1: Students in a govt.school study either English or Hindi as the main language.Let the %age of students studying English be 45% and %age of students studying Hindi be 75%. Considering that there is no compulsion for the students to study one of the two, solve the following parts.

Find the maximum %age of students who study both.

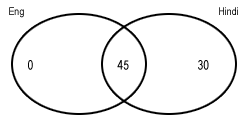
Take a look at the above Venn diagram. %age of students studying English is 45 and those studying Hindi is 75. As there is no compulsion to study one of the two, we can take 45 into the intersection section, making %age of students studying only English be 0%.
We have taken only English %age as 0% because if we increase it further, the %age of students studying both (the intersection region) will decrease.

b)Find the minimum %age of students studying both.
In this case, we'll make the total of the Venn diagram to 100%

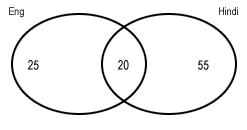
Wondering how we got 20%? Let's see.
Let us take English intersection Hindi to be = x
Students studying only English = 45-x
Students studying only Hindi = 75-x.
Making their sum=100%, we get 45-x+75-x+x=100 ⇒ x=20%.
c)Find the maximum no.of students studying exactly 1.
We will have maximum students studying exactly 1 when minimum no. of students study both.
In the second part of the question, we had calculated the minimum value of the students studying both.
Therefore, the required value will be equal to 100-20= 80%.
d)Find the minimum no.of students studying exactly 1.
We'll have minimum students studying exactly 1 when maximum no. of students study both.
Therefore, it will be equal to 75-45=30%.

a) Find the maximum %age of students who study both.

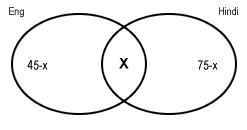
In this case, we will have to make the total of the three to be equal to 100%.
Making the total = 100, we get x=20%
Therefore, the required value will be 20%.
b) Find the minimum %age of students studying both.
This too shall be equal to 20%. (As the total will have to be = 100%)
c) Find the maximum no.of students studying exactly 1.
We'll have maximum students studying exactly 1 when minimum no. of students study both.
Therefore, it will be equal to 100-20 = 80%.
d) Find the minimum no.of students studying exactly 1.
We'll have minimum students studying exactly 1 when maximum no. of students study both.
Therefore, it will be equal to 100-20=80%.
So, this is all about maxima and minima in Venn Diagrams in the case of 2 variables. We'll discuss the concept of 3 variables in the next article.