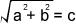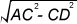In this article, we will discuss some basic concepts of geometry like Pythagoras theorem, commonly used Pythagorean triplets, conditions for acute and obtuse triangles and tricks to form a Pythagorean triplet. Let us go through these concepts one by one.
Pythagoras Theorem
The Pythagoras theorem states that, "the square of the hypotenuse (the side opposite the right angle) is equal to the sum of the squares of the other two sides".
The basic formula to calculate hypotenuse is a² + b² = c², where c represents the length of the hypotenuse and a and b are the lengths of the triangle's other two sides.
If the length of both a and b are known, then c can be calculated as
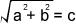
In this triangle, c2=a2 + b2
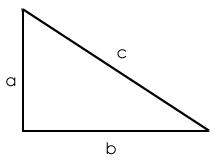
Although Pythagoras theorem is applicable in case of a right-angled triangle only, yet it has a lot of direct and indirect applications.
Classification of triangles on Pythagoras theorem:
- If a2 + b2 < c2, then the triangle would be an obtuse-angled triangle.
- If a2 + b2 > c2, then the triangle would be an acute-angled triangle.
Let us see its application in solving questions.
Example: Find the number of acute triangles that can be formed with two of its sides equal to 8, 15.
Solution: For an acute triangle, we have condition a2 + b2 > c2
Other condition that we'll use is: The sum of 2 sides in a triangle is greater than the third side.
Let the third side be x.
Applying the first condition, we get
82+x2 > 152; 82+152 >x2; x2+152>82
x2>225-64 ⇒ x2 >161 => Since x is an integer, x=13,14,15,16,17,....
82+152 >x2 ⇒ 289>x2 => x=0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16.
x2+15>82⇒x>0
Applying the second condition, we get
8+15>x; 8+x>15; 15+x>8
⇒x<23; x>7; x> -7
&rArr Combining the two conditions, we get x=13, 14, 15, 16.
Hence we get 4 cases. Answer= 4
How to Form a Pythagorean Triplet
- If the number is odd: Square the number N and then divide it by 2. Take the integer that is immediately before and after that number i.e. (N2/2 -0.5) and (N2/2 +0.5).
Pythagorean triplet= N, (N2/2 -0.5), (N2/2 +0.5)
Example: Take number N=3.
On squaring the number, we get 9.
Now take the half of it. 9/2= 4.5
The integer immediately before 4.5= 4; the integer immediately after 4.5= 5
Therefore, the triplet is 3, 4, 5.
- If the number is even: Take the half of that number N and then square it.
Pythagorean triplet= N, (N/2)2-1, (N/2)2+1
Example: Take number N=8
Half of N=4.
Pythagorean triplet= 8, (42-1), (42+1) i.e. 8, 15, 17
Note: If a, b, c is a Pythagorean triplet, then ka, kb, kc will also form a Pythagorean triplet; where k= integer. As (3, 4, 5) is a triplet, (6,8,10), (9,12,15),(12,16,20),...(30,40,50), all these will also be triplets.
Commonly Used Pythagorean Triplets
Three numbers which satisfy Pythagorean Theorem form a Pythagorean Triplets. Some commonly used Pythagorean triplets asked in the exams directly or indirectly are:
3,4,5; 5,12,13; 7,24,25; 9,40,41; 11,60,61; 12,35,37; 8,15,17; 28,45,53; 20,21,29; 16,63,65
Let us learn the application of Pythagorean triplets with the help of some examples.
Solved Examples
Example 1: Find the area of triangle with sides 12 cm, 35 cm, 37 cm.
Solution: We know that 12, 35, 37 is a Pythagorean triplet. So, the hypotenuse must be 37 i.e. longest side.
The rest 2 sides are perpendicular and base.
Area of triangle= ½ × Base × Height
Area of triangle = ½ × 12 × 35 = 210 cm²
Example 2: Find the area of a right-angled triangle of hypotenuse 91 cm and height 35 cm.
Solution: The given triangle is right-angled, so its sides must form a Pythagoras triplet.
We know (5, 12, 13) is a triplet, and by observing the lengths of the given side, there's a common factor i.e. 7.
When it is given that hypotenuse is 91 (i.e. 13 × 7) and height is 35 (i.e. 5 × 7), we can say that the base must be 12 × 7 = 84.
Area of triangle = ½ × Base × Height
⇒ ½ × 35 × 84 = 1470 cm2
Example 3: Find the area of rectangle ABCD.
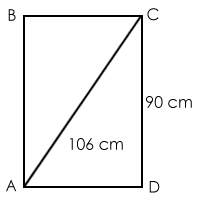
Solution: AD=
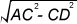
Solving this question involves complex calculation.
As (28, 45, 53) is a triplet, twice of that i.e. (56, 90, and 106) will also be a triplet.
As 90 and 106 are already given to us, the third side will be 56 (i.e. 28 × 2) because ∠ADC=90°, as ABCD is a rectangle.
So, AD=56 cm.
Area of rectangle = (56 × 90) = 5040 cm².
Key Learning:
- The use of Pythagorean triplets makes solving questions easy. Hence, it is of utmost importance that you memorize the commonly asked triplets shared in this article.
- If all the numbers in the triplet is multiplied by any constant number, then the resulting numbers would also make a Pythagorean Triplet.
- The condition for acute triangle (a2 + b2 > c2) and obtuse triangle (a2 + b2 < c2) finds application in many questions on geometry.
For doubts, post your comments below and our experts will provide you with the solutions.