Solved Examples of Mixture and Alligation

Please go through the following mixture and alligation problems to get a better understanding of fundamentals:

Example 1: If 60 pounds of nuts that cost Rs. 12 per pound are mixed with 20 pounds of nuts that cost Rs. 16 per pound, what is the cost per pound of the mixture?
Sol: Here the rule of alligation cannot be applied, as the average price is not given, but it is to be calculated. Now the normal average logic will be applied.
The total cost of the 80 pounds of nuts is 60 × 12 + 20 × 16 = Rs. 1040.
The cost per pound is 1040/80 = Rs. 13.

Example 2: A person has 6 litres of milk solution A which has 10 percent water in it and n litres of milk solution B which has 20 percent water in it. How many liters of solution B must he mix with solution A to obtain a milk solution 14 percent water .
Sol: Let us solve this question by both the methods i.e. the equation as well as alligation.
Here, n represent the number of litres of the 20 % solution. The amount of water in this 20 % solution [0.2n] plus the amount of water in the 10 % solution [(0.1) (6)] must be equal to the amount of water in the 14% mixture [0.14 (n + 6)].
Therefore, 0.2n + 0.1(6) = 0.14(n + 6) ⇒ 0.2n + 0.6 = 0.14n + 0.84  0.06n =0.24 ⇒ n = 4 liters.
4 liters of the 20% salt solution must be added to the 10% solution to obtain 14% solution. This question was solved with the help of equations. Now let us solve this question by alligation rule

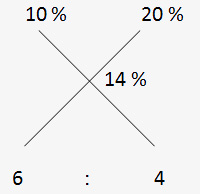
There are already 6 litres of 10 % solution, this means 4 litres of 20 % solution should be added.

Example 3: In a zoo there are goats and parrots. If their heads are counted, they are 180 while their legs are 448. Find the number of parrots.
Sol: As the total heads are 180 means these are 180 in number. If all of them are goats then the total number of legs would be 180 X 4 = 720. If all of them are parrots then the total number of legs are 180 X 2 = 360.
Now apply alligation and mixture method:
The mean number of legs is given to be 448.

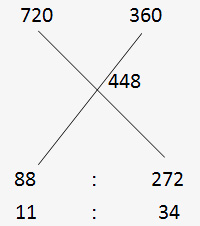
⇒ There are 180 X 34/45 = 136 parrots.

Example 4: Two vessels contain milk and water in the ratio of 3 : 1 and 5 : 3 respectively. Find the ratio in which these are to be mixed to get a new mixture in which the ratio of milk to water is 2 : 1.
Sol: In such questions, you should simply take one component out of the two given i.e. milk and water and then take its mean value and find the ratio.
Let us take milk. Milk is 3/4th in the first vessel and 5/8th in the second vessel and the average milk needed is 2/3rd.

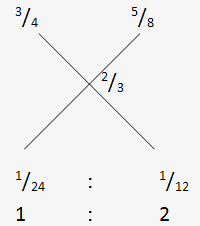
⇒ Ratio is 1 : 2 and this is the answer. If 1 litre is taken from the first vessel 2 litres should be taken from the second vessel.

Example 5: A tank has a mixture of milk and water in the ratio of 3: 1. What proportion of the mixture should be withdrawn and replaced with water so that the resulting mixture has equal proportions of milk and water?
Sol: Water is initially 1/4th of the total and what you are mixing in it is the water. Water has how much water in it (seems odd). But true, water has 100 % water in it (in percentage) or 1 time of water (in fractions). So the rule of alligation will be applied as,

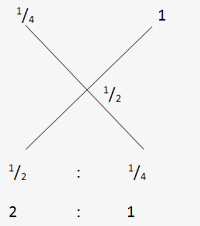
Now they are to mixed in the ratio of 2 : 1. It is also known that the proportion of water is actually by replacing the mixture, this means 1 out of a total of 3 (1 + 2) should be replaced i.e. 1/3rd of the total should be replaced.

Example 6: The vendor has two types of liquid solutions and he mixes them in ratio 5 : 3. The cost of first liquid is Rs 4 more than the other liquid. Find the cost price of each of the liquids if he gains 20 % on selling the mixed solution at Rs 12 per litre.
Sol: Let the cost of 1st liquid be x. Therefore, the cost of 2nd liquid = x – 4.
The cost of 8 litres of the mixture = 5x + 3(x – 4) = 8x – 12
Therefore, the cost of 1 litre (dividing the above calculated value by 8) of the mixture = x – 1.5
As the vendor gains 20 % by selling a litre of the mixture at Rs. 12, we get
(120/100) * (x-1.5) = 12
(12/10) (x-1.5) =12
Solving for “x”, we get, x = 11.5
Therefore, the costs of the liquids are Rs. 11.5 and Rs. 7.50 respectively.

Repeated dilution of a Mixture

One characteristic case in mixtures is the repeated dilution of a mixture with one of the ingredients, by removing, says n litres of the mixture and replacing it with n litres of one of the ingredients. Let there be m litres of water initially. Now, we remove n litres of the water and replace it by n litres of wine. This operation is done t times. Then
Quantity of water left in the vessel = m [1-(n/m)]^t
Where m = total quantity
n = quantity drawn every time
t = no. of times

Example 7: There are 80 litres of water in a vessel. 8 litres of water are withdrawn & replaced with milk, then 8 litres of mixture are withdrawn & replaced with milk. What is the quantity of water left in the mixture?
Sol: Water left in the vessel = 80(1 – 8/80)²
80 × 9/10 × 9/10 = 64.8 litres.