Q1. In a triangle ABC, AB = 9, BC = 10, AC = 13. Find the length of median AD. If G is the centroid, find GA and GD
A. 10/3, 5/3
B. 3/4, 8/5
C. 20/3, 10/3
D. 9/10, 8/3
Sol: Option C
Solution: By Apollonius theorem, AB
2 + AC
2
= 2 * (AD)
2 + 2 * (DC)
2
∴ 81 + 169 = 2 * (AD)
2 + 2 * (5)
2
∴ 250 = 2 * (AD)
2 + 2 * (5)
2
∴ 125 = AD
2 + 25…..(Dividing by 2)
∴ 100 = AD
2
∴ 10 = AD
∴ Median = 10.
Since G divides AD in the ratio 2: 1
So, GA = 2/3 * AD = 2/3 * 10 = 20/3,
GD = 1/3 * 10 = 10/3
Q2. ∆PQR is a right angled triangle, right angled at P & PS is the altitude to QR. If PQ = 8 and PS = 15, find QR and altitude PS. If T is the midpoint of QR, find PT.
A. 10.5
B. 8.5
C. 7.6
D. 9.25
Sol: Option B
By the theorem of Pythagoras, QR
2 = 8
2 + 15
2 = 64 + 225 = 289
∴ QR = √289 = 17
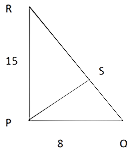
Area of the triangle = 1/2 * Product of perpendicular sides = ½ * 8 *15 = 60.
Also area = 1/2 * QR * PS = 60 = 1/2 * 17 * PS = 60
∴ PS = 120/17
Again, PT is the median to the hypotenuse.
∴ PT = 1/2 * hypotenuse = 1/2 * 17 = 8.5
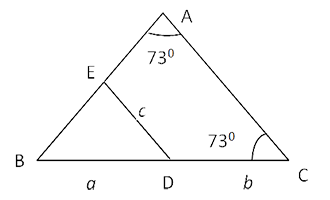
Q3. In the figure below, area of the cyclic quadrilateral AEDC is 28 sq. units. BD, DC and DE have lengths a, b, and c respectively that are in the ratio of 1: 2 : 3. Find the area of ∆ ABC.
A. 31.5 sq. units
B. 35sq.units
C. 32 sq. units
D. 33.75 sq. units
Sol: Option A

As ∠ A = ∠ C is cyclic quadrilateral AEDC
ED must be || to AC, Let a = x, b = 2x, c = 3x
∆ EBD is similar to ∆ABC
Ar(∆EBD) / Ar(∆ABC) = a
2 / (a+b)
2 = 1/9
If area ∆ EBD = A
⇒ Area ∆ ABC = 9A
Thus area of quadrilateral AEDC = 9A – A = 8A
8A = 28 Sq. units
⇒ ∆ ABC = 9A
= 31.5 sq units
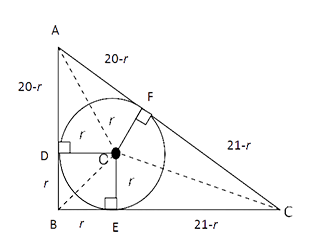
Q4. ∆ABC is a right angled triangle with ∠B = 90
0, AB = 20 cm and BC = 21cm. A circle with centre O is inscribed in ∆ABC. OD, OE, OF are perpendiculars drawn on the sides AB, BC and CA respectively. Find the ratio of the area of the quadrilateral FOEC to the area of quadrilateral ADOF.
A. 15:14
B. 14:15
C. 12:11
D. 7:5
Sol: Option A
AC= &redic;AB2 + BC2
∴(20 - r) + (21 - r) = 29 ⇒ r = 6
∆ OEC & ∆ OFC are congruent
Area of (Quad FOEC) ≡ 2 (Area ∆ OEC)
= 2 * 1/2 * 15 * 6
= 90 cm2
Similarly ∆ AOD & ∆ AOF are congruent ≡ ∆ AOF (RHS)
Area of (Quad ADOF) = 2 (Area ∆AOD)
= 2 * 1/2 * 14 * 6 = 84 cm2
Area(QuardFOEC) / Area(QuardADOF) = 90/84 = 15/14
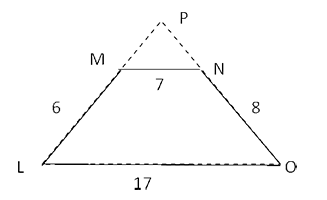
Q5. In the trapezium LMNO shown below, MN is parallel to LO. LM = 6, MN = 7, NO = 8, OL = 17. If the sides ON and LM are extended to meet at P, find the measure of ∠ LSO.
A. 100°
B. 90°
C. 60°
D. 120°
Sol: Option B
NS is drawn parallel to ML from N
⇒ NS = ML = 6, SO = LO – LS
= LP – MN = 17 – 7 = 10
In ∆ NSO, NS = 6, SO = 10, NO = 8
⇒ NSO is right angled at ∠ N
Thus ∠ SNO = 90 0
⇒ ∠ LPO = 90 0
Must Read Triangles Articles
Q6. In a ∆ ABC, two medians, AM of length 13 cm and BN of length 12cm intersect at point G. If the ∆ AGB so formed is a right angled triangle with AB as the hypotenuse, then find the area of ∆ ABC.
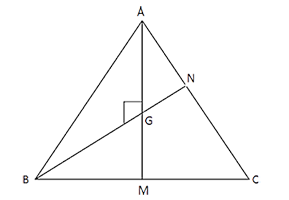
A. 120 cm2
B. 100 cm2
C. 104 cm2
D. 106 cm2
Sol: Option C
Centroid G divide median in the ratio of 2 : 1
AM = 13 ⇒ AG = 2/3 (13) = 26/3 cm
BN = 12 cm,
Area (∆ABN) = 1/2 * BN * AG = 1/2 * 12 * 26/3
= 52 cm2
Median BN divides ∆ABC into two triangle S of equal area
∴ Area (∆ABC) = 2(52) = 104 cm2
Q7. a,b, c are integers that are sides of an obtuse-angled triangle. If ab = 4, find c.
A. 1
B. 2
C. More than one possible value of c exists
D. 3
Sol: Option D
ab = 4
ab could be 4 * 1 or 2 * 2
221
223 these are the possible triangles.
222
441
44c is a triangle if c is 1.
22c will be a triangle if c is 1, 2 or 3 (trial and error).
- 221 is an acute. 12 + 22 > 22
- 222 is an equilateral. (acute)
- 223 is an obtuse. 22 + 22 < 32
- 144 is an acute. 12 + 42 > 42
Only the triangle 223 is obtuse. So, the third side has to be 3.
Q8. Perimeter of a triangle with integral sides is 15. How many such triangles can exist?
Sol: Option B
This is a counting question. Let us assume x ≤ y ≤ z.
The sum of two sides should be greater than the third.
x = 1, Possible triangle: 1, 7, 7
x = 2, possible triangle: 2, 6, 7
x = 3, possible triangles: 3, 5, 7 and 3, 6, 6
x= 4, possible triangles: 4, 5, 6 and 4, 4, 7
x = 5, possible triangle: 5, 5, 5
Therefore, there are 7 triangles possible.
Q9. What is the number of isosceles triangles with integral sides possible so that the sum of two sides of that triangle is 12?
Sol: Option D
Two possibilities: 2 equal sides could add up to 12 or sum of 2 unequal sides = 12.
i.e. Sum of two equal sides = 12
Sum of two unequal sides = 12
⇒ If sum of two equal sides were 12, sides of the triangle should be 6, 6, x.
What are the values that 'x' can take?
Value of x could range from 1 to 11.
So, 11 integer values exist.
⇒ 2 unequal sides adding to 12, could be: 1 + 11, 2 + 10, 3 + 9, 4 + 8 or 5 + 7.
So, how many isosceles triangles are possible with the above combinations?
There are six possibilities of isosceles triangles with the above combination are:
1, 11, 11
2, 10, 10
3, 9, 9
4, 8, 8
5, 7, 7
5, 5, 7
⇒ Triplets such as (1, 1, 11), (2, 2, 10), etc are eliminated as the sum of two smaller values is less than the largest value. These cannot form a triangle.
So, 11 + 6 = 17 possibilities.
Q10. A triangle ABC right–angled at B has inradius 2 cm & circumradius of 7 cm. Find the area of the triangle ABC?
A. 31.5
B. 32
C. 33
D. 32.5
Sol: Option A
r = 2
R = 7 =(1/2 of hypotenuse)
Hypotenuse= 14
r =(a+b−h)/2
2 =(a+b−14)/2
a + b – 14 = 4
a + b = 18
a2+ b2= 142
a2+ (18 – a)2= 196
a2+ 324 + a2– 36a = 196
2a2– 36a + 128 = 0
a2– 18a + 64 = 0
Now the 2 roots of this equation will effectively be a, 18 – a. Product of the roots = 64.
Therefore, Area =1/2* product of roots = 32 sq. cms





