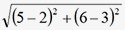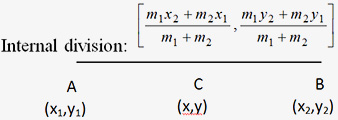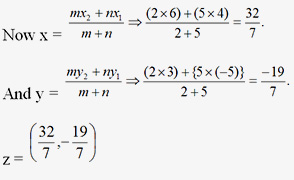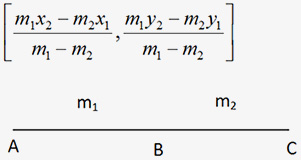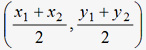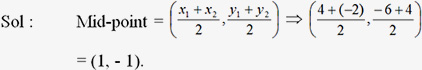A coordinate graph consists of a rectangular grid with two crossing lines called axes. The x-axis is the horizontal line and the y-axis is the vertical line. The axes intersect each other at the point (0,0) which is also called the origin.
Operations that can be done in Coordinate Geometry
If we are given the coordinates of some points we can:
- Calculate the distance between them
- Finding the midpoint, slope or equation of a line segment
- Determine if the given set of lines are parallel or perpendicular
- Finding the area or perimeter of a given polygon defined by the points..
- Define the equations of different geometric figures.
For 2 lines having equations:
a1x+b1y=c1
a2x+b2y=c2
Unique Solution (meet at a single point) = (a1 / a2) ≠ (b1 / b2)
No solutions (does not meet) = (a1 / a2) = (b1 / b2) ≠ (c1 / c2)
Infinitely many solution (overlapping) = (a1 / a2) = (b1 / b2) = (c1 / c2)
Given below is a graph showing which coordinates are having what signs in different quadrants?
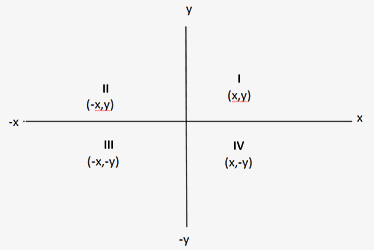
1. Distance Formula between A (x1, y1) & B (x2, y2).
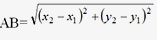
Example: Find the distance between two Points: A (2,3) and B(5,6)?
Using the above formula:
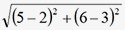
The answer comes out to be 3&redic;2.
2. The coordinates of C dividing the line segment joining the points (x1,y1) & (x2,y2) internally in the ratio
m1:m2 are
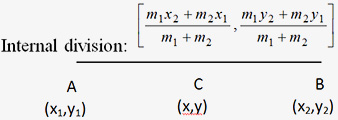
Example .Find the co-ordinates of point Z, which divides the join of P (4, -5) and Q (6, 3) internally in the ratio 2 :5
Sol: Let the co-ordinates of point Z are (x, y).
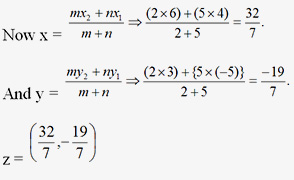
3. External Division
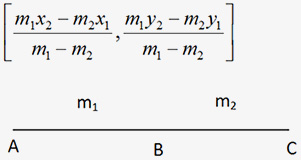
Must Read Co-ordinate Geometry Articles
4. Equal ratio
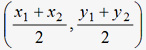 Example:
Example: Find the co-ordinates of the mid-point of the line segment joining the points M (4, -6) and N (-2, 4).
Different forms associated with the equations:
1. The point slope form: The equation of a straight line passing through the point.(x1,y1) and having slope m is (y-y1)=m(x-x1)
2. Two point form:

3. Slope intercepts form: The equation of a line having slope m & making an intercept C on y axis is : y=mx+C
Example: Find the equation of the line parallel to the line passing through (5, 7) and (2, 3) and having x intercept as -4.
Sol: Slope of the given line = (7 - 3) / (5 - 2) = 4/3. So the slope of the required line is also 4/3. One point on this line is (-4, 0). Hence the equation of the line is:
y - 0 = 4/3 (x + 4) ⇒ 3y = 4x +16.
4. Double intercept form :
(x/a) + (y/b) = 1
5. General form of an equation is Ax+By+C=0
6. For Parallel lines(slopes are equal) i.e. m1 =m2
7. For perpendicular Lines(product of slopes = -1) m1*m2 =-1
Example:
What is the relation between different set of given lines:
a) y = 3x + 1
b) y = -1/3 x + 2
c) 1/3y = x - 3
The gradients of the lines are 3, -1/3 and 3 respectively. Therefore (a) and (b) and perpendicular, (b) and (c) are perpendicular and (a) and (c) are parallel.
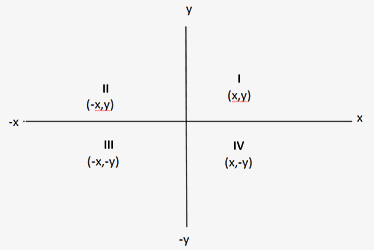
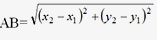 Example: Find the distance between two Points: A (2,3) and B(5,6)?
Example: Find the distance between two Points: A (2,3) and B(5,6)?