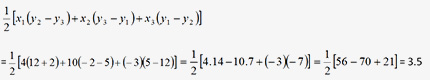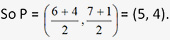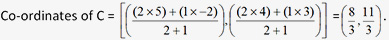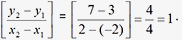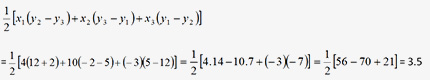Example 1. In which quadrant does the point (-3,4) lie?
1. 1st quadrant
2. 2nd quadrant
3. 3rd quadrant.
4. 4th quadrant
Sol: Option 2
The point is negative in the x axis and positive for the y axis , thus the point must lie in the 2nd quadrant.
Example 2. Find the co-ordinates of a point on x-axis, which is at a distance of 5 units from the point (6, -3).
1. (2, 0) and (10, 0).
2. (0,2) and ( 0,10).
3. (2, 10) and (0, 0).
4. None of these
Sol: Option 1
Let the co-ordinates of the point on the x-axis be (x, 0).
As distance =&redic;(x2 - x1)2 + (y2 - y1)2,
so 5 = &redic;(x-6)2 + (0-(-3))2
⇒ 25 = x2 - 12x + 36 + 9.
⇒ x = 2 or x = 10
So the required points are (2, 0) and (10, 0).
Example 3. The quadrants where abcissa and ordinate have different signs are?
1. 1st & 2nd quadrant
2. 2nd & 3rd quadrant
3. 1st & 3rd quadrant
4.2nd & 4th quadrant
Sol: Option 2
The signs are different for 2nd and 4th quadrants.
Example 4. Find the co-ordinates of the point of intersection of the medians of triangle MNO; given M = (-2, 3), N = (6, 7), O = (4, 1).
1. (5/3 , 1/3)
2. (3/8 , 3/11)
3. (8/3 , 11/3)
4. (5/3 , 17/3)
Sol: Option 3
Point of intersection of medians is called as centroid, at which each median is divided in the ratio 2 : 1. Firstly find the midpoint of NO and take it as P
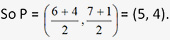
Take the point C, where medians meet and it will divide the median MP in the ratio 2: 1.
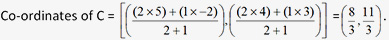
Example 5. What is the slope of the line passing through the points J (-2, 3) and (2, 7)?
Sol: Option 2
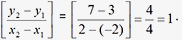
Must Read Co-ordinate Geometry Articles
Example 6. Find the equation of the line whose slope is 2 and y intercept is - 3.
1. y =2/3x- 1
2. Y=3x-2
3. Y=2x-3
4. None of these
Sol: Option 3
Given m = 2 and c = - 3. Substituting values in y = mx + c, we get y = 2x – 3.
Example 7. Find the equation of the line passing through (2, -1) and parallel to the line 2x – y = 4.
1. y=2/5x- 1
2. Y=5x-2
3. Y=2x-5
4. None of these
Sol: Option 3
The given line is 2x – y = 4 ⇒ y = 2x – 4 (Converting into the form of y = mx + c)
Its slope = 2. The slope of the parallel line should also be 2.
Hence for the required line
m = 2 and (x1 , y1) = (2, -1).
Equation = (y-y1) / (x/x1) = (y2-y1) / (x2-x1)
⇒ (y-y1) / (x/x1) = m
⇒ y-y1 = m (x-x1) ⇒ y - (-1) = 2(x-2)
⇒ y = 2x – 5.
Example 8. Find the coordinate of the point which will divide the line joining the point (2, 4) and (7,9) internally in the ratio 1:2?
1. (5/3 , 1/3)
2. (3/8 , 3/11)
3. (8/3 , 11/3)
4. (11/3 , 17/3)
Sol: Option 4
The internal division will use the formula (mx2 + nx1 )/ (m + n)
y = (my2 + ny1 )/(m + n).
So, the point becomes (11/3,17/3).
Example 9. Find the coordinates of the point which will divide the line joining the points (3, 5) and (11, 8) externally in the ratio 5: 2.
1. (5/3 , 1/3)
2. (3/49 , 1/10)
3. (49/3 , 10)
4.None of these
Sol: Option 4
The external division case will use the formula
x = (mx2 – nx1 )/(m – n)
y = (my2 – ny1 )/ (m – n)
where m:n is 5:2 in our case.
Putting the values you will get points (49/3, 10).
Example 10. Find the equation of straight line passing through (2, 3) and perpendicular to the line 3x + 2y + 4 = 0
1. y =5/3x- 2
2. 3Y=2x+5
3. 3Y=5x-2
4. None of these
Sol: Option 2
The given line is 3x + 2y + 4 = 0 or y = (-3x/2) - 2
Any line perpendicular to it will have slope = 2/3
Thus equation of line through (2, 3) and slope 2/3 is
(y – 3) = 2/3 (x – 2)
⇒ 3y – 9 = 2x – 4
⇒ 3y – 2x – 5 = 0.
Example 11. Find the area of the triangle formed by the vertices (4, 5), (10, 12) and (-3, 2)
Sol: Option 4
The area of the triangle having its vertices as P(x1, y1), Q(x2, y2) and R(x3, y3) is given by